Giải câu 5 trang 106 toán VNEN 8 tập 1
Câu 5: Trang 106 toán VNEN 8 tập 1
Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
a) Tứ giác ADFE là hình gì? Vì sao?
b) Tứ giác EMFN là hình gì? Vì sao?
Bài làm:
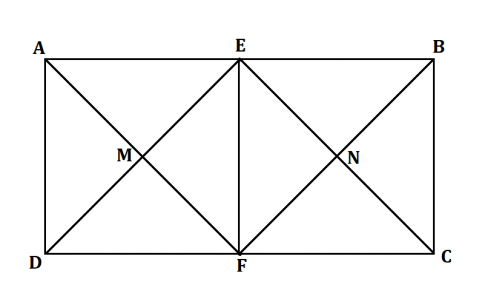
a) Vì E là trung điểm AB nên AE = EB = ![]() AB
AB
Mà AB = 2AD hay ![]() AB = AD $\Rightarrow$ AE = AD. (1)
AB = AD $\Rightarrow$ AE = AD. (1)
Xét hình chữ nhật ABCD, có: E là trung điểm AB và F là trung điểm CD
![]() EF là đường trung bình của hình chữ nhật ABCD
EF là đường trung bình của hình chữ nhật ABCD ![]() EF // AD
EF // AD
Lại có AD ![]() DC và AD
DC và AD ![]() AB $\Rightarrow$ EF
AB $\Rightarrow$ EF ![]() DF và EF
DF và EF ![]() AE
AE
![]() AEFD là hình chữ nhật. (2)
AEFD là hình chữ nhật. (2)
Từ (1) và (2) ![]() AEFD là hình vuông.
AEFD là hình vuông.
b) Tứ giác DEBF có EB // DF và EB = DF nên AEBF là hình bình hành ![]() DE // BF hay ME // NF.
DE // BF hay ME // NF.
Chứng minh tương tự, ta có: AF // EC hay MF // EN.
![]() MENF là hình bình hành. (3)
MENF là hình bình hành. (3)
Theo câu a, ADFE là hình vuông nên ME = MF và ME ![]() MF. (4)
MF. (4)
Từ (3) và (4) ![]() EMFN là hình vuông.
EMFN là hình vuông.
Xem thêm bài viết khác
- Giải câu 3 trang 54 toán VNEN 8 tập 1
- Giải câu 3 trang 80 toán VNEN 8 tập 1
- Giải câu 1 trang 19 toán VNEN 8 tập 1
- Giải câu 4 trang 43 sách VNEN toán 8 tập 1
- Giải VNEN toán 8 bài 7: Luyện tập
- Giải câu 4 trang 120 toán VNEN 8 tập 1
- Giải câu 1 trang 48 toán VNEN 8 tập 1 phần C
- Giải câu 1 trang 54 toán VNEN 8 tập 1
- Giải câu 1 trang 22 toán VNEN 8 tập 1
- Giải VNEN toán đại 8 bài 2: Tính chất cơ bản của phân thức
- Giải VNEN toán 8 bài 8: Phép chia các phân thức đại số
- Giải câu 2 trang 93 toán VNEN 8 tập 1











