Giải câu 1 trang 101 toán VNEN 8 tập 1

D. Hoạt động vận dụng

Câu 1: Trang 101 toán VNEN 8 tập 1

a) Chứng minh rằng: Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB.

b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A, B) thì tam giác ABC vuông tại C.

Bài làm:

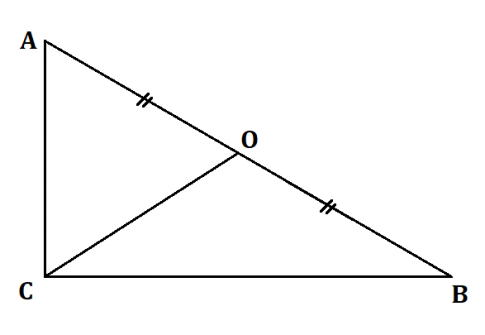
a) Gọi O là trung điểm của AB.

Ta có CO là trung tuyến ứng với cạnh huyền AB nên OC = AB hay OA = OB = OC.

A, B, C cùng thuộc trên một đường tròn bán kính OA.

Vậy C thuộc đường tròn đường kính AB.

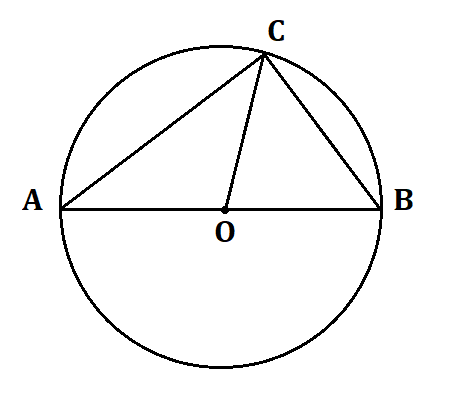
b) Gọi O là tâm đường tròn.

Tam giác ABC có trung tuyến CO bằng nửa cạnh AB (do CO = AO = BO) nên tam giác ABC vuông tại C.