Giải câu 7 trang 115 toán VNEN 9 tập 2

Câu 7: Trang 115 toán VNEN 9 tập 2

Cho tam giác ABC vuông tại A. Lấy điểm D bất kì thuộc cạnh AB. Đường tròn (O) đường kính DB cắt CD tại điểm E và cắt AE tại điểm G. Chứng minh rằng AB là tia phân giác của .

Hướng dẫn: Xem hình 105

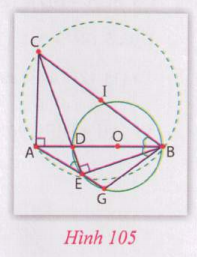
Theo giả thiết có vì góc nội tiếp chắn nửa đường tròn. Suy ra CAEB là tứ giác nội tiếp, vì hai đỉnh A và E cùng nhìn cạnh BC dưới một góc vuông.

Khi đó, , vì $...$

Do DEGB là tứ giác nội tiếp nên

Từ đó suy ra , hay $.......$

Bài làm:

Theo giả thiết có vì góc nội tiếp chắn nửa đường tròn. Suy ra CAEB là tứ giác nội tiếp đường tròn I (I là trung điểm của BC), vì hai đỉnh A và E cùng nhìn cạnh BC dưới một góc vuông.

Khi đó, , vì góc nội tiếp đường tròn (I) chắn cung AC

Do DEGB là tứ giác nội tiếp nên

Từ đó suy ra , hay BA là tia phân giác $\widehat{CBG}$.