Giải câu 8 đề 1 ôn thi toán lớp 9 lên 10

1 Đánh giá

Bài 8. (3,0 điểm)

Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Đường thắng AH cắt BC và (O) lần lượt tại F và K (K # A).

Gọi L là hình chiếu của D lên AB.

a. Chứng minh rằng tứ giác BEDC nội tiếp và $BD^{2} = BL.BA$

b. Gọi J là giao điểm của KD và (O), (J # K). Chứng minh BJK = BDE

c. Gọi I là giao điểm của BJ và ED. Chứng minh tứ giác ALIJ nội tiếp và I là trung điểm của ED.

Bài làm:

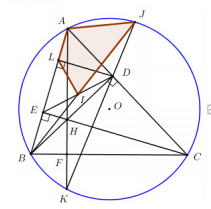
a. Xét tứ giác BEDC có:

$\angle BEC = 90^{0} (do CE\perp AB)$

$\angle BDC = 90^{0} (do BD\perp AC)$

Suy ra $\angle BEC=\angle BDC(90^{0})$ nên tứ giác BEDC có hai đỉnh E, D kề nhau cùng nhìn cạnh BC dưới các góc vuông, do đó tứ giác BEDC là tứ giác nội tiếp.

b. Xét tam giác ABC có hai đường cao BD và CE cắt nhau tại H nên H là trực tâm tam giác ABC hay $AH\perp BC$ ó $AF\perp BC$

Xét tam giác EBC vuông tại E có $\angle EBC + \angle BCE= 90^{0}$ (1)

Xét tam giác AFB vuông tại F có $\angle FBA + \angle BAF= 90^{0}$ (2)

Từ (1) và (2) suy ra $\angle BCE= \angle BAK$ (3) (cùng phụ với $∠ A B F$ )

Mà theo câu a ta có tứ giác BEDC là tứ giác nội tiếp nên $\angle BDE=\angle BCE$ (4)

Từ (3) và (4) suy ra $\angle BDE=\angle BAK$ (*)

Xét đường tròn (O) có $\angle BAK=\angle BJK$ (**) (hai góc nội tieeos cùng chắn cung BK)

Từ (*) và (**) ta suy ra $\angle BJK=\angle BDE$ (đpcm)

c.

Xét tam giác BDJ và tam giác BID có:

$\angle BJK = \angle BDE$ (cmt)

$\angle DBJ$ chung

$\Delta BDJ\sim \Delta BID (g.g)\Rightarrow \frac{BD}{BI}=\frac{BJ}{BD}\Rightarrow BI.BJ=BD^{2}$

Lại có $BD^{2}=BL.BA$ (cmt)

$\Rightarrow BL.BA=BI.BJ\Rightarrow \frac{BL}{BJ}=\frac{BI}{BA}$

Xét tam giác BLI và tam giác BJA có:

$\frac{BL}{BI}=\frac{BI}{BA}$ (cmt)

$\angle ABJ$ chung

=> $\Delta BLI\sim \Delta BJA (c.g.c)$

$\Rightarrow \angle BLI = \angle BIA$ (hai góc tương ứng)

=> Tứ giác ALIJ là tứ giác nội tiếp (tứ giác có góc goài bằng hóc trong tại đỉnh đối diện.

Tứ giác BEDC là tứ giác nội tiếp (cmt) $\Rightarrow \angle AED = \angle BJA$ (6)

Từ (5) và (6) $\Rightarrow \angle BLI=\angle AED$ hay $∠ E L I = ∠ L E I \Rightarrow Δ I L D$ cân tại I => IL = ID.

Ta có:

$\angle ILD = 90^{0}$

$\angle IDL = 90^{0}$

$\Rightarrow \angle ILD = \angle IDL\Rightarrow \Delta ILD$ cân tại I => IL = ID

Vậy IE = ID => I là trung điểm của ED (dpcm)

132 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Ôn toán 9 lên 10