Lời giải bài 2 chuyên đề Bài toán Dựng hình

Bài 2: Dựng tam giác ABC với trung tuyến AM có độ dài bằng một đoạn thẳng m cho trước ,và các góc MAB và MAC lần lượt bằng những góc và $\beta$ cho trước.

Bài làm:

Phân tích :

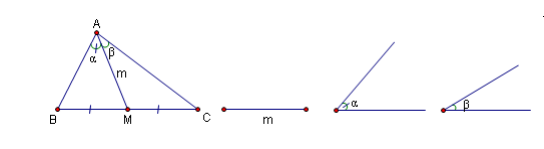
Giả sử bài toán đã giải xong và ta đã dựng được tam giác ABC thoả mãn yêu cầu bài toán .Hình vẽ trên cho thấy không có một bộ phận nào của hình hội đủ điều kiện để dựng được.

Ví dụ: Tam giác AMC chỉ có hai yếu tố được biết là và AM = m ,nên không thể dựng được.Khi này nhớ lại những bài toán tương tự .

Bài toán :nếu kéo dài trung tuyến AM thêm một đoạn MD = AM ,thì hai tam giác AMB và DMC bằng nhau (c.g.c) .

=> .

=> Từ đó ,hình thành tam giác ACD với và AD = 2m. Tam giác đó hội đủ điều kiện để dựng được .

Sau khi dựng được tam giác này ,ta sẽ dựng được điểm B .

Cách dựng hình :

• Dựng đoạn thẳng AD = 2m.
• Dựng hai góc kề cạnh đó là , hai cạnh AC và DC giao nhau tại C.
• Sau đó ta vẽ trung tuyến CA của tam giác ACD và kéo dài thêm một đoạn MB =MC , từ đó xác định đỉnh B của tam giác ABC cần dựng .

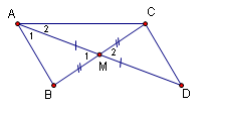
Chứng minh :

Theo cách dựng này ,rõ ràng tam giác AMB và tam giác DMC bằng nhau(c.g.c).

Nên ta có :

• 
• .

Vậy tam giác ABC dựng được thoả mãn đầy đủ các yêu cầu đề bài .

Biện luận :

Trên đây ta nói hai cạnh AC và DC giao nhau tại C.Thực ra là chúng chỉ giao nhau nếu .

Do đó bài toán luôn giải được và có một nghiệm hình.