Giải câu 4 đề 5 ôn thi toán lớp 9 lên 10
Câu 4: (3,5 điểm)
Cho nửa đường tròn tâm O, đường kính AB = 2R. Đường thẳng qua O và vuông góc với AB cắt cung AB tại C. Gọi E là trung điểm của đoạn thẳng BC, AE cắt nửa đường tròn tâm O tại F (F khác A). Đường thẳng qua điểm C và vuông góc với AF tại G cắt AB tại H.
a. Chứng minh tức giác CGOA nội tiếp. Tính số đo của góc OGH
b. Chứng minh OG là tia phân giác của góc COF
c. Chứng minh hai tam giác CGO và CFB đồng dạng.
Bài làm:
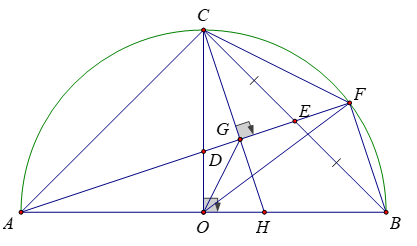
a. Xét tứ giác ACGO có:
∠CGA = ![]() (CG ⊥ AG)
(CG ⊥ AG)
∠COA = ![]() (CO ⊥ AO)
(CO ⊥ AO)
=> 2 đỉnh G và O cùng nhìn CA dưới 1 góc bằng nhau
=> Tứ giác ACGO là tứ giác nội tiếp
b. Tứ giác ACGO là tứ giác nội tiếp
=> ∠COG = ∠CAG (2 góc nội tiếp cùng chắn cung CG)
Mà ∠CAG = ![]() (góc nội tiếp bằng nửa góc ở tâm cùng chắn 1 cung)
(góc nội tiếp bằng nửa góc ở tâm cùng chắn 1 cung)
=> ∠COG = ![]()
=> OG là tia phân giác của góc ∠COF
c. Xét (O): ∠FCB = ∠FAB (2 góc nội tiếp cùng chắn cung FB)
Tứ giác ACGO là tứ giác nội tiếp
=> ∠OCG = ∠FAB (2 góc nội tiếp cùng chắn cung GO)
=> ∠FCB∠ = ∠OCG
Xét ΔCGO và ΔCFB có:
∠OCG = ∠FCB
∠GOC = ∠FBC (= ∠CAF )
=> ΔCGO ∼ ΔCFB (g.g)
d) Gọi D là giao điểm của CO và AE
Xét tam giác CAB có:
CO là trung tuyến
AE là trung tuyến
CO giao AE tại D
=> D là trọng tâm của tam giác CAB.
![]()
Xét tam giác AOD vuông tại O có:

Xét ΔAOD và ΔAFB có:
∠FAB là góc chung
∠AOD = ∠AFB = 90o
=> ΔAOD ∼ ΔAFB

![]()
![]()
![]() (đpcm)
(đpcm)
Xem thêm bài viết khác
- Giải câu 5 đề 11 ôn thi toán lớp 9 lên 10
- Đáp án đề thi vào lớp 10 môn Toán Kiên Giang năm 2022 Đề thi môn Toán vào lớp 10 Kiên Giang năm 2022
- Giải câu 3 đề 16 ôn thi toán lớp 9 lên 10
- Đề thi thử vào lớp 10 môn Toán thành phố Hà Nội năm 2022 - Đề 12 Đề thi thử vào lớp 10 môn Toán 2022
- Giải câu 4 đề 12 ôn thi toán lớp 9 lên 10
- Giải câu 5 đề 5 ôn thi toán lớp 9 lên 10
- Giải câu 3 đề 18 ôn thi toán lớp 9 lên 10
- Giải câu 3 đề 7 ôn thi toán lớp 9 lên 10
- Đề thi thử vào lớp 10 môn Toán phòng GD Ứng Hòa năm 2022 Đề thi thử vào lớp 10 môn Toán 2022
- Đề thi thử vào 10 môn Toán phòng GD Kim Sơn năm 2022 Đề thi thử vào 10 môn Toán 2022
- Đề thi thử vào 10 môn Toán trường THCS Nguyễn Công Trứ năm 2022 Đề thi thử vào 10 môn Toán 2022
- Đề thi thử vào lớp 10 môn Toán THCS Đồng Phú năm 2022 Đề thi thử vào lớp 10 môn Toán 2022











