Lời giải Bài 2-Một số bài toán Hình học thường gặp trong đề tuyển sinh vào 10 năm 2017

Bài làm:

Lời giải chi tiết :

Đề ra :

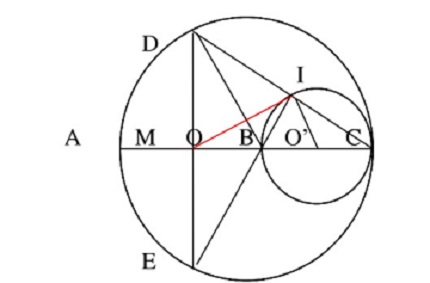
Cho ( O ) , đường kính AC .Trên OC lấy điểm B và vẽ đường tròn ( O' ) ,đường kính BC .Gọi M là trung điểm AB .Từ M vẽ dây cung DE vuông góc với AB , DC cắt (O') tại I .

a. Tứ giác ADBE là hình gì ?

b. Chứng minh : DMBI nội tiếp .

c. Chứng minh : B , I , C thẳng hàng và MI = MD .

d. Chứng minh : MC. DB = MI . DC

e. Chứng minh : MI là tiếp tuyến của (O') .

Hướng dẫn giải :

a.

Ta có :

=> DM = ME

=> Tứ giác ADBE là hình bình hành .

Mặt khác , ta có : BD = BE ( AB là đường trung trực của DE )

=> Tứ giác ADBE là hình thoi .

b. Ta có :

• BC là đường kính
• 

=>

Và :

=>

=> Tứ giác DMBI nội tiếp . ( đpcm )

c.

Vì AEBD là hình thoi => BE // AD

Mà : ( góc nội tiếp chắn nửa đường tròn )

=> (1)

Ta có :

=> (2)

Từ (1) , (2) => B , I , E thẳng hàng . ( đpcm )

Ta có :

=> MI là đường trung tuyến của tam giác vuông DEI .

=> MI = MD . ( đpcm )

d.

Xét và $\triangle DCB$ , ta có :

• chung
• ( cùng chắn cung MI )

=>

=> ( đpcm )

e.

+ Ta có : cân => $\widehat{O'IC}=\widehat{O'CI}$

Mặt khác : Tứ giác MBID nội tiếp => ( cùng chắn cung MB )

+ Ta có: cân tại B => $\widehat{MDB}=\widehat{MEB}$

Và : Tứ giác MECI nội tiếp => ( cùng chắn cung MI )

=>

=>

=> tại I nằm trên đường tròn (O')

Vậy MI là tiếp tuyến của (O') . ( đpcm )