Lời giải Bài 3 Đề thi thử lên lớp 10 môn toán lần 2 năm 2017 của Trường THPT chuyên Vinh

Bài làm:

Lời giải bài 3 :

Đề bài :

Cho tam giác đều ABC và M là một điểm bất kỳ trên BC.Gọi D , E lần lượt là hình chiếu vuông góc của M trên AB và AC .Xác định vị trí của điểm M để tam giác MDE có chu vi nhỏ nhất .

Hướng dẫn giải chi tiết :

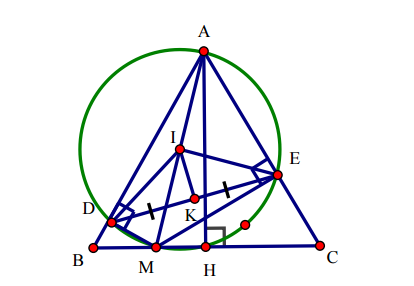
Ta có : Chu vi tam giác MDE = MD + ME + DE.(BM + CM ). +DE = BC. + DE

Mà ( BC. ) luôn không đổi

=> Chu vi tam giác MDE nhỏ nhất khi và chỉ khi DE nhỏ nhất .

Xét tứ giác ADME nội tiếp đường tròn đường kính AM ( ) ,nên tam giác ADE cũng nội tiếp đường tròn đường kính AM,tâm I là trung điểm AM .

Gọi K là trung điểm DE =>

Mà

=>

Khi đó để DE nhỏ nhất <=> AM nhỏ nhất <=> ( H là chân đường vuông góc hạ từ A xuống BC , và tam giác ABC đều (gt) => HB = HC ).

Vậy khi M là trung điểm BC thì chu vi tam giác MDE nhỏ nhất.