Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 4 năm 2017 của trường THPT chuyên Sư Phạm Hà Nội

Bài làm:

Lời giải bài 4 :

Đề bài :

Cho đường tròn O đường kính BC và một điểm A nằm bất kì trên đường tròn ( A khác B và C ). Gọi AH là đường cao của DABC, đường tròn tâm I đường kính AH cắt các dây cung AB, AC tương ứng tại D, E.

a. Chứng minh rằng : góc và AB. AD = AC . AE .

b. Các tiếp tuyến của đường tròn (I) tại D và E cắt BC tương ứng tại G và F. Tính số đo góc GIF .

c. Xác định vị trí điểm A trên đường tròn (O) để tứ giác DEFG có diện tích lớn nhất .

Hướng dẫn giải chi tiết :

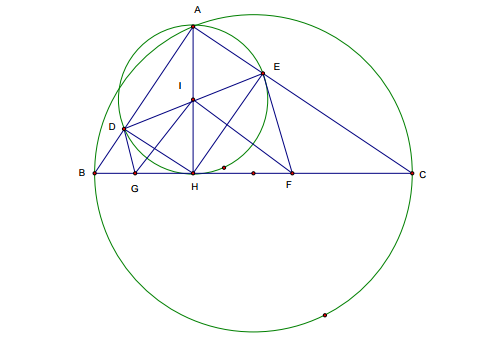
a. Tứ giác ADHE có :

=> ADHE là hình chữ nhật .

=> ( đpcm ) .

Xét hai tam giác vuông HAB và HAC ta có : ( hệ thức lượng trong tam giác vuông )

Mà :

=> AB. AD = AC . AE . ( đpcm )

b. Vì => DE là đường kính => $I\in DE$ .

=>

Mà : ( nhìn hình vẽ ) .

=> .

Vậy .

c. Tứ giác DEFG là hình thang vuông có đường cao DE = AH

Hai đáy DG = GH = GB = và EF = FC = FH = $\frac{1}{2}HC$

=> Diện tích hình tứ giác DEFG là :

Để đạt giá trị lớn nhất khi AH lớn nhất ( Vì BC = 2R - không đổi ) .

Khi đó AH sẽ phải là đường kính => A là trung điểm của cung AB .

Vậy A là trung điểm của cung AB trên đường tròn (O) thì tứ giác DEFG có diện tích lớn nhất .