Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên Amtesdam Hà Nội

Bài làm:

Lời giải bài 4:

Đề ra :

Cho đường tròn (O, R) , dây BC cố định và . Điểm A di động trên cung lớn BC sao cho ∆ ABC nhọn. Hai đường cao BM và CN cắt nhau tại H. Gọi D là điểm đối xứng với B qua M và E là điểm đối xứng với C qua N. Đường tròn $(O_1;R_1)$ ngoại tiếp ∆ ABD và đường tròn $(O_2;R_2)$ ngoại tiếp ∆ ACE cắt nhau tại điểm thứ hai K.

1. Chứng minh rằng tứ giác BHCK nội tiếp.

2. Chứng minh rằng và ba điểm E, B, K thẳng hàng.

Lời giải chi tiết :

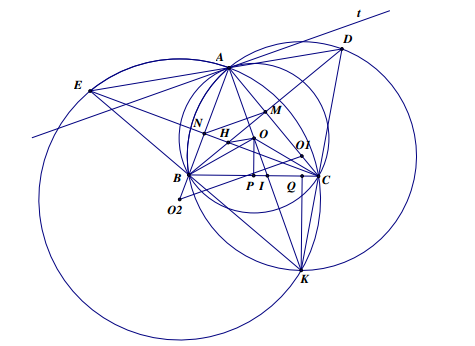
1. Ta có :

=>

=>

Xét ( ) ta có :

• 
• ( ∆ ABD cân tại A )

=>

=>

Tương tự :

=>

=>

=> Tứ giác BHCK nội tiếp. ( đpcm )

2. Theo bài ra :

Kẻ tiếp tuyến At của (O) tại A => ( cùng bù với $\widehat{MNC}$ )

Mà : => $\widehat{AMN}=\widehat{tAC}$

=> At // MN .

Mặt khác , ta có :

Vì : => AK là phân giác $\widehat{BKC}$ . (1)

Ta có :

=> Tứ giác BOCK nội tiếp , OB = OC => .

=> KO là phân giác . (2)

Từ (1) , (2) => A , O , K thẳng hàng .

Mà :

=> . ( đpcm )

Ta có :

=>

=> E , B , K thẳng hàng ( đpcm ) .