Lời giải Bài 4 Đề thi thử trường THPT chuyên Amtesdam Hà Nội
Bài làm:
Lời giải bài 4:
Đề ra :
Từ một điểm A nằm ngoài đường tròn (O;R) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm) và một cát tuyến AMN ( M nằm giữa A và N). Gọi I, K, P lần lượt là hình chiếu vuông góc của M xuống các cạnh AB, AC, BC. Gọi E là điểm chính giữa cung nhỏ BC.
a) Chứng minh: AIMK là tứ giác nội tiếp đường tròn.
b) Gọi H là trung điểm đoạn BC. Chứng minh: AM.AN = AH. AO.
c) Chứng minh E là tâm đường tròn nội tiếp tam giác ABC.
Lời giải chi tiết :
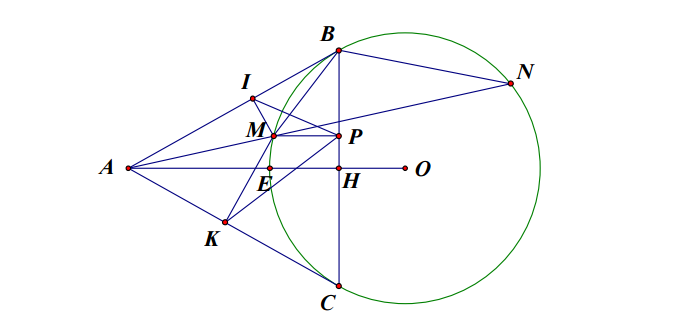
a. Ta có : ![]()
=> ![]()
=> Tứ giác AIMK là tứ giác nội tiếp đường tròn . ( đpcm )
b. Xét ![]() ( g-g )
( g-g )
=> ![]() (*)
(*)
Xét ![]() vuông tại B có BH là đường cao .
vuông tại B có BH là đường cao .
=> ![]() (**)
(**)
Từ (*),(**) => AM.AN = AH. AO. ( đpcm )
c. Vì E là điểm chính giữa cung nhỏ BC ( gt )
=> ![]()
=> AE là phân giác trong của góc BAC . (1)
Ta có : ![]()
=> BE là phân giác trong của góc ABC . (2)
Từ (1) , (2) => E là tâm đường tròn nội tiếp tam giác ABC. ( đpcm )
Xem thêm bài viết khác
- Lời giải Câu 4 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên Lê Qúy Đôn
- Lời giải Câu 1 Đề thi thử lên lớp 10 môn toán năm 2017 của trường THPT chuyên Nguyễn Trãi
- Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên Nguyễn Huệ
- Lời giải Câu 4 Đề thi thử lên lớp 10 môn toán lần 2 năm 2017 của trường THPT chuyên Lê Qúy Đôn
- Lời giải Bài 3 Đề thi thử lên lớp 10 môn toán lần 2 năm 2017 của Trường THPT chuyên Vinh
- Lời giải Bài 5 Đề thi thử lên lớp 10 môn toán lần 3 năm 2017 của trường THPT chuyên Nguyễn Huệ
- Lời giải Bài 5 Đề thi thử lên lớp 10 môn toán lần 2 năm 2017 của trường THPT chuyên Nguyễn Huệ
- Đề thi thử lên lớp 10 môn toán năm 2017 của trường THPT chuyên Nguyễn Trãi
- Lời giải Bài 5 Đề thi thử lên lớp 10 môn toán lần 3 năm 2017 của trường THPT chuyên TP HCM
- Lời giải Bài 2 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của Trường THPT chuyên Vinh
- Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 4 năm 2017 của Trường chuyên Lam Sơn Thanh Hóa
- Lời giải Bài 2 Đề thi thử lên lớp 10 môn toán lần 3 năm 2017 của Trường THPT chuyên Vinh











