-
Tất cả
-
 Tài liệu hay
Tài liệu hay
-
 Toán Học
Toán Học
-
 Soạn Văn
Soạn Văn
-
Soạn đầy đủ
- Tiếng Việt 2 tập 2 KNTT
- Tiếng Việt 2 CTST
- Tiếng Việt 2 sách Cánh Diều
- Tiếng Việt 3 tập 2
- Tiếng Việt 3 tập 1
- Tiếng Việt 4 tập 2
- Tiếng Việt 4 tập 1
- Tiếng Việt 5 tập 2
- Tiếng Việt 5 tập 1
- Soạn văn 6
- Soạn văn 7
- Soạn văn 8 tập 1
- Soạn văn 8 tập 2
- Soạn văn 9 tâp 1
- Soạn văn 9 tập 2
- Soạn văn 10 tập 1
- Soạn văn 10 tập 2
- Soạn văn 11
- Soạn văn 12
-
Soạn ngắn gọn
- Soạn văn 12 ngắn gọn tập 1
- Soạn văn 12 ngắn gọn tập 2
- Soạn văn 11 ngắn gọn tập 1
- Soạn văn 11 ngắn gọn tập 2
- Soạn văn 10 ngắn gọn tập 1
- Soạn văn 10 ngắn gọn tập 2
- Soạn văn 9 ngắn gọn tập 1
- Soạn văn 9 ngắn gọn tập 2
- Soạn văn 8 ngắn gọn tập 1
- Soạn văn 8 ngắn gọn tập 2
- Soạn văn 7 ngắn gọn tập 1
- Soạn văn 7 ngắn gọn tập 2
- Ngữ văn VNEN
- Đề thi THPT QG môn Ngữ Văn
-
Soạn đầy đủ
-
 Tiếng Anh
Tiếng Anh
-
 Vật Lý
Vật Lý
-
 Hóa Học
Hóa Học
-
 Sinh Học
Sinh Học
-
 Lịch Sử
Lịch Sử
-
 Địa Lý
Địa Lý
-
 GDCD
GDCD
-
 Khoa Học Tự Nhiên
Khoa Học Tự Nhiên
-
 Khoa Học Xã Hội
Khoa Học Xã Hội
-
Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên Sư Phạm Hà Nội
Bài làm:
Lời giải bài 4 :
Đề bài :
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của . tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) ( với F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Biết AF =![]() .
.
a) Chứng minh tứ giác OBDF nội tiếp. Định tâm I đường tròn ngoại tiếp tứ giác OBDF.
b) Tính ![]() .
.
c) Kẻ OM ⊥ BC ( M ∈ AD) . Chứng minh : ![]() .
.
Hướng dẫn giải chi tiết :
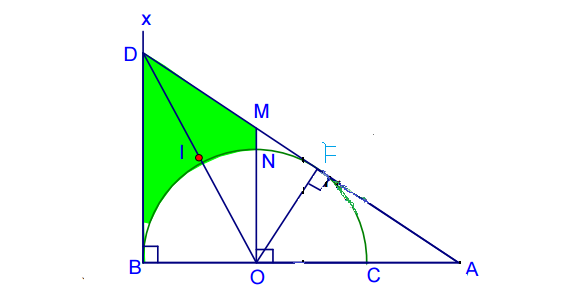
a. Ta có : ![]() ,$\widehat{DFO}=90^{\circ}$ (t/c tiếp tuyến)
,$\widehat{DFO}=90^{\circ}$ (t/c tiếp tuyến)
=> ![]()
=> Tứ giác OBDF nội tiếp đường tròn. (đpcm)
=> Khi đó Tâm I của đường tròn ngoại tiếp tứ giác OBDF chính là trung điểm của OD ( IO = ID ).
b. Áp dụng địn lý Py- ta-go cho tam giác OFA vuông ở F , ta có :
![]()
=> ![]()
Mà ![]()
=> ![]()
=> ![]() .
.
c. Ta có : OM // BD (![]() )
)
=> ![]() ( so le trong )
( so le trong )
![]() ( t/c 2 tiếp tuyến cắt nhau )
( t/c 2 tiếp tuyến cắt nhau )
=> ![]()
Vậy tam giác MOD cân tại M => MD = MO .
Áp dụng hệ quả định lí Talet cho tam giác ABD , ta có :
![]()
<=> ![]()
<=> ![]() (đpcm) .
(đpcm) .
Xem thêm bài viết khác
- Lời giải Bài 4 Đề thi thử trường THPT chuyên Đà Nẵng
- Lời giải Bài 2 Đề thi thử lên lớp 10 môn toán lần 2 năm 2017 của trường THPT chuyên TP HCM
- Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 3 năm 2017 của trường THPT chuyên Sư Phạm Hà Nội
- Lời giải Bài 3 Đề thi thử lên lớp 10 môn toán lần 2 năm 2017 của Trường chuyên Lam Sơn Thanh Hóa
- Lời giải Bài 2 Đề thi thử lên lớp 10 môn toán lần 3 năm 2017 của trường THPT chuyên Sư Phạm Hà Nội
- Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 Trường chuyên Lam Sơn Thanh Hóa
- Lời giải Bài 2 Đề thi thử lên lớp 10 môn toán lần 3 năm 2017 của Trường THPT chuyên Vinh
- Lời giải Bài 5 Đề thi thử lên lớp 10 môn toán lần 2 năm 2017 của Trường THPT chuyên Thái Bình
- Lời giải Bài 3 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên Sư Phạm Hà Nội
- Lời giải Bài 4 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên Sư Phạm Hà Nội
- Lời giải Câu 5 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên Lê Qúy Đôn
- Lời giải Bài 1 Đề thi thử lên lớp 10 môn toán lần 1 năm 2017 của trường THPT chuyên TP HCM











