Lời giải bài số 7, 9, 21 đề thi thử THPT Quốc gia môn toán năm 2017 của Sở Giáo dục và đào tạo tỉnh Hưng Yên
Bài làm:
Câu 7: Trong không gian với hệ trục tọa độ 0xyz, cho mặt phẳng (P): ![]() và ba điểm $A(1,-2,0), B(1,0,-1), C(0,0,-2)$. Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB, AC, BC?
và ba điểm $A(1,-2,0), B(1,0,-1), C(0,0,-2)$. Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB, AC, BC?
A. 1 mặt cầu.
B. Vô số mặt cầu.
C. 4 mặt cầu.
D. 2 mặt cầu.
Giải: Đáp án C
Phương trình mặt phẳng (ABC): 2x-y-2z-4=0
Giả sử mặt cầu cần tìm có tâm I, bán kính R.
Gọi H, K, T, J lần lượt là hình chiếu của I lên AB, AC, BC, (ABC).
Theo tính chất tiếp xúc, ta có R=IH=IK=IT.
Suy ra 3 tam giác vuông ![]() do đó JH=JK=JT suy ra J là tâm đường tròn nội tiếp hoặc bàng tiếp tam giác ABC. Vậy có 4 điểm J như vậy và ta sẽ có 4 điểm I tương ứng là hình chiếu của I lên (P). Tức là có 4 mặt cầu thỏa mãn.
do đó JH=JK=JT suy ra J là tâm đường tròn nội tiếp hoặc bàng tiếp tam giác ABC. Vậy có 4 điểm J như vậy và ta sẽ có 4 điểm I tương ứng là hình chiếu của I lên (P). Tức là có 4 mặt cầu thỏa mãn.
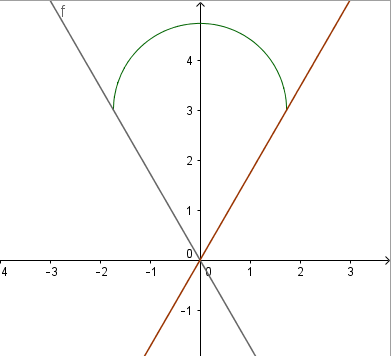
Câu 9: Cho hình phẳng (H) gồm nửa hình tròn đường kính AB và tam giác đều ABC như hình vẽ. Gọi ![]() là đường thẳng qua C và song song với AB. Biết $AB=2 \sqrt{3} cm$. Tính thể tích khối tròn xoay tạo bởi hình (H) và trục
là đường thẳng qua C và song song với AB. Biết $AB=2 \sqrt{3} cm$. Tính thể tích khối tròn xoay tạo bởi hình (H) và trục ![]() .
.

A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Giải: Đáp án C
Chọn ![]() , khi đó ta có tọa độ $A(-\sqrt{3},3), B(\sqrt{3},3)$ và phương trình đường tròn đường kính AB là $x^{2}+(y-3)^{2}=3$ và AC: $y=-\sqrt{3}x$, AB: $y=\sqrt{3}x$.
, khi đó ta có tọa độ $A(-\sqrt{3},3), B(\sqrt{3},3)$ và phương trình đường tròn đường kính AB là $x^{2}+(y-3)^{2}=3$ và AC: $y=-\sqrt{3}x$, AB: $y=\sqrt{3}x$.
Phần phía trên của nửa đường tròn có phương trình ![]()
Vì tính đối xứng của hình vẽ nên $V=2 \pi \int_{-\sqrt{3}}^{0} |(3+\sqrt{3-x^{2}})^{2}-(-\sqrt{3}x)^{2}|dx=16 \sqrt{3} \pi +9 \pi^{2}.
Câu 21: Cho hàm số ![]() liên tục trên $\mathbb{R}$ và có đồ thị của hàm số $y=f'(x)$ như hình vẽ
liên tục trên $\mathbb{R}$ và có đồ thị của hàm số $y=f'(x)$ như hình vẽ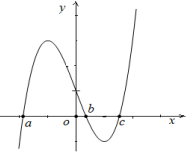
Chọn khẳng định đúng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Giải: Đáp án B
Chú ý theo định nghĩa tích phân và dựa vào đồ thị của hàm số, ta có diện tích của các hình phẳng:
![]()
![]()
![]() .
.
Xem thêm bài viết khác
- Đáp án Đề thi thử THPT quốc gia môn toán năm 2017 của Sở GD và ĐT Bắc Ninh
- Đề 9: Luyện thi THPTQG môn Toán năm 2018
- Đề và đáp án môn Toán tất cả các mã đề thi THPT quốc gia năm 2017
- Lời giải bài số 39, 42, 48 Đề thi thử THPT quốc gia môn toán năm 2017- Đề tham khảo số 1
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 106
- Đề thi thử THPT quốc gia môn toán năm 2017- Đề tham khảo số 8
- Lời giải bài số 32, 36, 47 Đề thi thử THPT quốc gia môn toán năm 2017- Đề tham khảo số 5
- Đề và đáp án môn Toán mã đề 107 thi THPT quốc gia năm 2017 đáp án của bộ GD-ĐT
- Đề 6: Luyện thi THPTQG môn Toán năm 2018
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 105
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 121
- Đề và đáp án môn Toán mã đề 113 thi THPT quốc gia năm 2017 đáp án của bộ GD-ĐT











