Giải câu 2 trang 106 toán VNEN 8 tập 1

Câu 2: Trang 106 toán VNEN 8 tập 1

Giải các bài toán sau:

a) Cho hình chữ nhật DEGH. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh DE, EG, GH, HD. Chứng minh rằng MNPQ là hình thoi.

b) Cho hình thoi PQRS. Gọi A, B, C, D tương ứng là các trung điểm của các cạnh PQ, QR, RS, SP. Chứng minh rằng ABCD là hình chữ nhật.

c) Cho hình vuông ABCD. Gọi U, V, T, Z tương ứng là các trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng UVTZ là hình vuông.

Bài làm:

a)

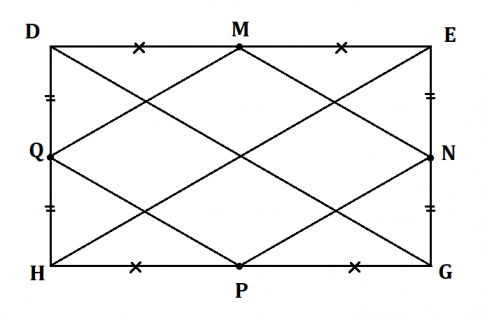
Xét DMQ, có: M là trung điểm DE và Q là trung điểm DH

MQ là đường trung bình của $\Delta$DMQ QM = $\frac{1}{2}$EH. (1)

Xét HEG, có: N là trung điểm EG và P là trung điểm HG

PN là đường trung bình của $\Delta$HEG PN = $\frac{1}{2}$EH. (2)

Từ (1) và (2) QM = PN = $\frac{1}{2}$EH. (*)

Chứng minh tương tự, ta có: QP = MN = DG. (**)

Mà DEGH là hình chữ nhật nên HE = DG.(***)

Từ (*), (**) và (***) MNPQ là hình thoi (đpcm).

b)

Xét QPR, có: A là trung điểm PQ và B là trung điểm QR

AB là đường trung bình của $\Delta$QPR AB // PR. (1)

Xét PSR, có: D là trung điểm PS và C là trung điểm SR

CD là đường trung bình của $\Delta$PSR CD // PR. (2)

Từ (1) và (2) AB // CD // PR. (*)

Chứng minh tương tự, ta có: AD // BC // QS. (**)

Mà PQRS là hình thoi nên QS PR (***)

Từ (*), (**) và (***) ABCD là hình chữ nhật (đpcm).

c)

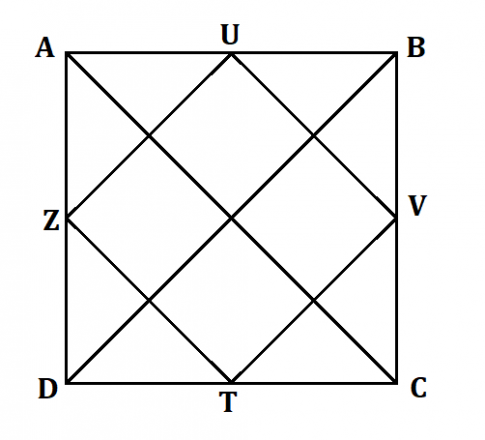
Xét ADB, có: Z là trung điểm AD và U là trung điểm AB

ZU là đường trung bình của $\Delta$ABD ZU // BD và ZU = $\frac{1}{2}$BD. (1)

Xét BCD, có: V là trung điểm BC và T là trung điểm DC

VT là đường trung bình của $\Delta$BCD TV // BD và TV = $\frac{1}{2}$BD. (2)

Từ (1) và (2) ZU // BD // TV và TV = ZU = $\frac{1}{2}$BD. (*)

Chứng minh tương tự, ta có: UV // ZT // AC và UV = ZT = AC. (**)

Mà ABCD là hình vuông nên AC BD và AC = BD (***)

Từ (*), (**) và (***) UVTZ là hình vuông (đpcm).