Giải câu 3 đề 3 ôn thi toán lớp 9 lên 10

1 Đánh giá

Bài 3: (2,0 điểm)

Cho (P): $y = \frac{-x^{2}}{4}$ và đường thẳng $(d): y = m(x - 1) - 2$

a. Vẽ đồ thị (P)

b. Chứng minh: (d) luôn cắt (P) tại hai điểm phân biệt A và B khi m thay đổi. Gọi $x_{A}$ ,$x_{B}$ lần lượt là hoành độ của A và B .Xác định m để $x_{A}^{2}x_{B} + x_{B}^{2} x_{A}$ đạt giá trị nhỏ nhất và tính giá trị đó?

Bài làm:

a. (P): $y = \frac{-x^{2}}{4}$

Bảng giá trị:

$x$	-4	-2	0	2	4
$y = \frac{-x^{2}}{4}$	-4	-1	0	1	4

Đồ thị (P) là đường Parabol nằm phía dưới trục hoành, nhận Oy làm trục đối xứng và nhận điểm O (0;0) làm đỉnh và điểm cao nhất

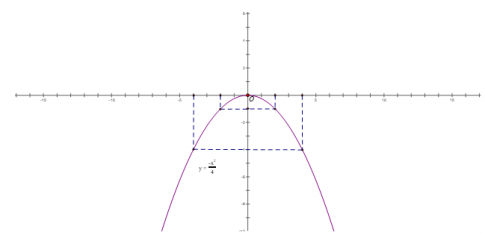
b. Phương trình hoành độ giao điểm của (P) và (d) là:

$\frac{-x^{2}}{4}= m(x - 1) -2$

$\Leftrightarrow x^{2}+4mx - 4m - 8 = 0$

$\Delta '=(2m)^{2}-(-4m-8)=4m^{2}+4m + 8 = 4 (m+1)^{2}+4$ > 0∀m

> Phương trình luôn có 2 nghiệm phân biệt hay (d) cắt (P) tại 2 điểm phân biệt A, B có hoành độ là $x_{A}$ ; $x_{B}$.

Theo định lí Vi-et ta có:

$\left\{\begin{matrix}x_{A}+x_{B}= -4m& & \\x_(A)x_(B)= -4m - 8 & & \end{matrix}\right.$

$x_{A}^{2}x_{B}+x_{B}^{2}x_{A}=x_{A}x_{B}(x_{A}+x_{B})= (-4m-8).(-4m)$

$=16m^{2}+32m = 16(m+1)^{2}-16$

Ta có: $16(m+1)^{2}\geq 0 ∀m$

$\Rightarrow 16(m+1)^{2}-16\geq -16∀m$

Dấu bằng xảy ra khi $m+1=0\Leftrightarrow m=-1$

Vậy GTNN của biểu thức là -16, đạt được khi m = -1.

31 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Ôn toán 9 lên 10