Giải câu 3 trang 101 toán VNEN 8 tập 1
Câu 3: Trang 101 toán VNEN 8 tập 1
a) Cho hình bình hành ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác MNPQ là hình gì? Vì sao?
b) Cho hình chữ nhật GHIK. Gọi X, Y, Z, T lần lượt là trung điểm của các cạnh GH, HI, IK, KG. Tứ giác XYZT là hình gì? Vì sao?
Bài làm:
a)
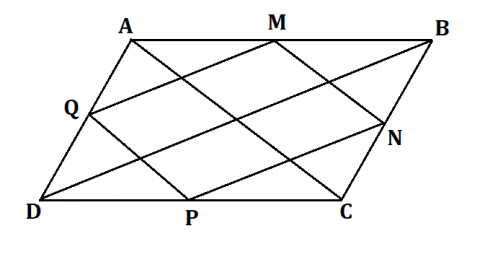
Xét tam giác ABD, có: M là trung điểm AB và Q là trung điểm AD
![]() QM là đường trung bình của tam giác ABD
QM là đường trung bình của tam giác ABD ![]() QM // BD. (1)
QM // BD. (1)
Xét tam giác BCD, có: N là trung điểm BC và P là trung điểm CD
![]() NP là đường trung bình của tam giác BCD
NP là đường trung bình của tam giác BCD ![]() PN // BD. (2)
PN // BD. (2)
Từ (1) và (2) ![]() QM // PN. (*)
QM // PN. (*)
Chứng minh tương tự, ta có QP // MN. (**)
Từ (*) và (**) ![]() MNPQ là hình bình hành.
MNPQ là hình bình hành.
b)
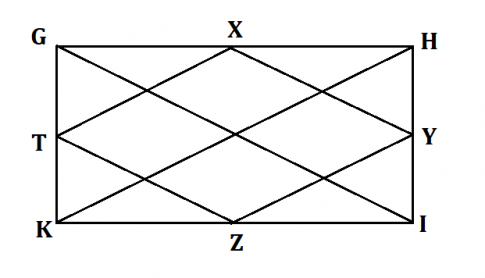
Xét tam giác GHK, có: X là trung điểm GH và T là trung điểm GK
![]() TX là đường trung bình của tam giác ABD
TX là đường trung bình của tam giác ABD ![]() TX = $\frac{1}{2}$KH. (1)
TX = $\frac{1}{2}$KH. (1)
Xét tam giác KHI, có: Y là trung điểm HI và Z là trung điểm KI
![]() YZ là đường trung bình của tam giác KHI
YZ là đường trung bình của tam giác KHI ![]() YZ = $\frac{1}{2}$KH. (2)
YZ = $\frac{1}{2}$KH. (2)
Từ (1) và (2) ![]() TX = YZ = $\frac{1}{2}$KH. (*)
TX = YZ = $\frac{1}{2}$KH. (*)
Chứng minh tương tự, ta có XY = TZ = ![]() GI.(**)
GI.(**)
Mà GHIK là hình chữ nhật nên KH = GI. (***)
Từ (*), (**), (***) ![]() XY = YZ = ZT = TX
XY = YZ = ZT = TX ![]() XYZT là hình thoi.
XYZT là hình thoi.
Xem thêm bài viết khác
- Giải VNEN toán 8 bài 2: Diện tích hình tam giác
- Giải câu 7 trang 132 toán VNEN 8 tập 1
- Giải câu 1 trang 101 toán VNEN 8 tập 1
- Giải câu 3 trang 58 toán VNEN 8 tập 1 phần D. E
- Giải câu 3 trang 84 toán VNEN 8 tập 1
- Giải câu 1 trang 60 toán VNEN 8 tập 1
- Giải câu 2 trang 7 toán VNEN 8 tập 1
- Giải câu 1 trang 47 toán VNEN 8 tập 1
- Giải câu 2 trang 127 sách Toán Vnen 8 tập 1
- Giải câu 1 trang 130 toán VNEN 8 tập 1
- Giải câu 3 trang 17 toán VNEN 8 tập 1
- Giải VNEN toán 8 bài 1: Đường thẳng song song với một đường thẳng cho trước











