Giải câu 3 trang 106 toán VNEN 9 tập 1

Câu 3: Trang 106 sách VNEN 9 tập 1

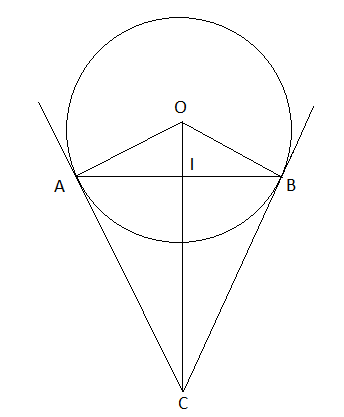
Cho đường tròn (O), dây AB khác đường kính, lấy I là trung điểm của AB. Đường thẳng OI cắt tiếp tuyến tại A của đường tròn ở điểm C.

a) Chứng minh CB là tiếp tuyến của đường tròn.

b) Cho bán kính của đường tròn bằng 13cm, AB = 24ccm. Tính độ dài OC.

Bài làm:

a) Ta có I là trung điểm của AB nên OI AB mà $\mathrm{\Delta }$ OAB cân tại O nên OI là phân giác của $\widehat{AOB}$

Xét OAC và OBC có:

OC chung, OA = OB, = $\widehat{BOC}$

$\mathrm{\Delta }$OAC = $\mathrm{\Delta }$OBC $\widehat{OBC}$ = $\widehat{OAC}$ = ${90}^{\circ }$

Suy ra CB là tiếp tuyến của (O).

b) AI = AB = .24 = 12cm

OI = $\sqrt{O{A}^2-A{I}^2}$ = $\sqrt{{13}^2-{12}^2}$ = 5cm

Áp dụng hệ thức lượng trong tam giác vuông OBC ta có:

= OI.OC $\Rightarrow$ OC = $\frac{O{A}^2}{OI}$ = $\frac{{13}^2}{5}$ = $\frac{169}{5}$cm

Vậy OC = cm.