Giải câu 3 trang 145 toán VNEN 8 tập 1

Câu 3: Trang 145 toán VNEN 8 tập 1

Cho hình bình hành ABCD có diện tích S. Gọi M, N tương ứng là trung điểm của AB và BC. Tính theo S diện tích tứ giác DMBN.

Bài làm:

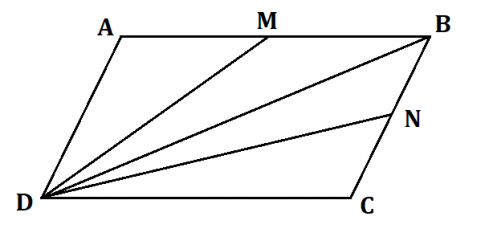
Ta có: BM = AB $\Rightarrow$ S$_{BDM}$ = S$_{ABD}$ (cùng chiều cao).

Tương tự, ta cũng có: BN = BC $\Rightarrow$ S$_{BDN}$ = S$_{BCD}$ (cùng chiều cao).

Như vậy: S + S$_{BDN}$ = $\frac{1}{2}$S$_{ABD}$ + $\frac{1}{2}$S$_{BCD}$

Hay S = $\frac{1}{2}$S$_{ABCD}$ = $\frac{1}{2}$S.