Giải câu 3 trang 54 sách toán VNEN lớp 8 tập 2

1 Đánh giá

Câu 3: Trang 54 sách VNEN 8 tập 2

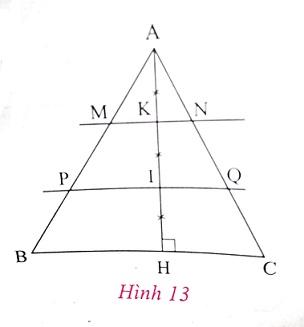
Tam giác ABC có BC = 18cm. Trên đường cao AH lấy các điểm I,K sao cho AK = KI = IH. Qua I và K lần lượt vẽ các đường PQ // BC, MN // BC (h.13).

a) Tính độ dài các đoạn thẳng MN và PQ.

b) Tính diện tích tứ giác MNPQ, biết rằng diện tích của $\Delta$ ABC là 360 $c m^{2}$ .

Bài làm:

a) * Vì MN // BC theo định lí Ta-lét ta có:

$\frac{MN}{BC}$ = $\frac{A M}{A B}$

Vì MK // BH theo định lí Ta-lét ta có:

$\frac{AM}{AB}$ = $\frac{A K}{A H}$ = $\frac{1}{3}$

$\Rightarrow$ $\frac{M N}{B C}$ = $\frac{A M}{A B}$ = $\frac{1}{3}$

$\Rightarrow$ MN = $\frac{1}{3}$ .BC = $\frac{1}{3}$ .18 = 6cm.

* Vì PQ // BC theo định lí Ta-lét ta có:

$\frac{PQ}{BC}$ = $\frac{A P}{A B}$

Vì PI // BH theo định lí Ta-lét ta có:

$\frac{AP}{AB}$ = $\frac{A I}{A H}$ = $\frac{2}{3}$

$\Rightarrow$ $\frac{P Q}{B C}$ = $\frac{A P}{A B}$ = $\frac{2}{3}$

$\Rightarrow$ PQ = $\frac{2}{3}$ .BC = $\frac{2}{3}$ .18 = 12cm.

b) Ta có:

S $\Delta$ AMN = $\frac{1}{2}$ .AK.MN

S $\Delta$ ABC = $\frac{1}{2}$ .AH.BC

$\Leftrightarrow$ $\frac{S Δ A M N}{S Δ A B C}$ = $\frac{\frac{1}{2} . A K . M N}{\frac{1}{2} . A H . B C}$ = $\frac{A K}{A H}$ . $\frac{M N}{B C}$ = $\frac{1}{3}$ . $\frac{6}{18}$ = $\frac{1}{9}$

$\Leftrightarrow$ S $Δ$ AMN = $\frac{1}{9}$ .S $Δ$ ABC = $\frac{1}{9}$ .360 = 40 $c m^{2}$

$\Rightarrow$ Diện tích tứ giác MNQP = S $Δ$ ABC - S $Δ$ AMN = 360 - 40 = 320 $c m^{2}$

Vậy diện tích tứ giác MNQP là 320 $cm^{2}$

22 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Toán VNEN 8 tập 2