Giải câu 4 đề 8 ôn thi toán lớp 9 lên 10

Bài 4: (3,5 điểm)

Cho hình vuông ABCD có hai đường chéo cắt nhau tại E. Lấy I thuộc cạnh AB, M thuộc cạnh BC sao cho: (I và M không trùng với các đỉnh của hình vuông).

a. Chứng minh rằng BIEM là tứ giác nội tiếp đường tròn

b. Tính số đo của góc

c. Gọi N là giao điểm của tia AM và tia DC; K là giao điểm của BN và tia EM. Chứng minh .

Bài làm:

Hình vẽ:

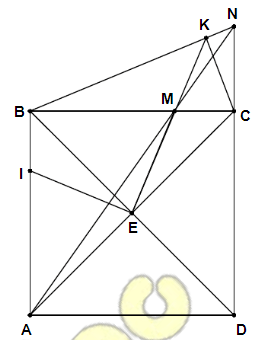
a. Tứ giác BIEM có: (gt); suy ra tứ giác BIEM nội tiếp đường tròn đường kính IM.

b. Tứ giác BIEM nội tiếp suy ra: (do ABCD là hình vuông)

c. và $\mathrm{\Delta }ECM$ có:

, suy ra $MB=IA$

Vì: CN// BA nên theo định lí thalet, ta có:

Suy ra IM song song với BN (định lí thalet đảo).

. Lại có $\widehat{BCE}={45}^0$ (do ABCD là hình vuông).

Suy ra: là tứ giác nội tiếp.

Suy ra: mà $\widehat{BEC}={90}^0$, suy ra $\widehat{BKC}={90}^2$ hay $CK\perp BN$.