Giải câu 4 trang 114 toán VNEN 8 tập 1
Câu 4: Trang 114 toán VNEN 8 tập 1
Cho hình thang ABCD có BC // AD và AB = BC = CD = a, AD = 2a. Gọi E là trung điểm của AD.
a) Cho biết số đo các góc của hình thang đó.
b) Chứng minh rằng ABCE và BCDE là các hình thoi.
c) Chứng minh rằng ACD và ABD là các tam giác vuông.
d) Gọi M, N tương ứng là trung điểm của AE và ED. Chứng minh rằng BCNM là hình chữ nhật.
Bài làm:
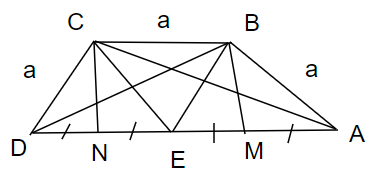
a) E là trung điểm AD => DE = EA = a
- Tứ giác ABCE có: BC // AE và BC = AE = a => ABCE là hình bình hành
- Mà BC = AB = a => ABCE là hình thoi.
=> CE = CB = a (Tính chất của hình thoi). (1)
- Chứng minh tương tự có tứ giác BCDE là hình thoi => BE = BC = a. (2)
- Từ (1) và (2) => CE = BE (= BC = a)
- Xét tam giác CEB có CE = CB = EB = a => ![]() CEB đều => $\widehat{CEB}=\widehat{CBE}=\widehat{ECB}=60^{0}$
CEB đều => $\widehat{CEB}=\widehat{CBE}=\widehat{ECB}=60^{0}$
- Xét tam giác CDE có CD = CE = DE = a => ![]() CDE đều => $\widehat{CDE}=\widehat{CED}=\widehat{ECD}=60^{0}$
CDE đều => $\widehat{CDE}=\widehat{CED}=\widehat{ECD}=60^{0}$
- Tương tự ta có ![]() BEA đều (BE = AB = EA = a) => $\widehat{BEA}=\widehat{BAE}=\widehat{EBA}=60^{0}$
BEA đều (BE = AB = EA = a) => $\widehat{BEA}=\widehat{BAE}=\widehat{EBA}=60^{0}$
=> Số đo các góc của hình thang:
![]() ;
;
![]()
b) Theo chứng minh ở phần a ta có: Tứ giác ABCE và BCDE là hình thoi.
c) ABCE là hình thoi có AC là đường chéo => AC là tia phân giác của góc BAE => ![]()
Xét tam giác ACD có: ![]()
=> ![]()
=> Tam giác ACD vuông tại C.
Chứng minh tương tự ta được tam giác ABD vuông tại B.
d) M là trung điểm của AE, N là trung điểm của ED => NE = EM = ![]() => NM = a => NM = BC (= a)
=> NM = a => NM = BC (= a)
Tứ giác CBMN có: NM = BC và NM // BC => CBNM là hình bình hành.
Ta có tam giác CDE là tam giác đều (chứng minh phần a) => CN là đường trung tuyến => CN cũng là đường phân giác của góc DCE
=> ![]()
Xét tam giác ECN có: ![]()
=> ![]()
Hình bình hành CBNM có ![]() (có một góc vuông)=> CBMN là hình chữ nhật
(có một góc vuông)=> CBMN là hình chữ nhật
Xem thêm bài viết khác
- Giải câu 4 trang 17 toán VNEN 8 tập 1
- Giải VNEN toán 8 bài 8: Chia đơn thức cho đơn thức, chia đa thức cho đơn thức
- Tình huống 2 trang 70 VNEN toán 8 tập 1
- Giải câu 3 trang 10 toán VNEN 8 tập 1
- Giải câu 4 trang 106 toán VNEN 8 tập 1
- Giải câu 6 trang 59 toán VNEN 8 tập 1
- Giải câu 2 trang 29 toán VNEN 8 tập 1
- Giải câu 5 trang 127 toán VNEN 8 tập 1
- Giải câu 4 trang 59 toán VNEN 8 tập 1
- Giải VNEN toán 8 bài 7: Luyện tập
- Giải câu 3 trang 106 toán VNEN 8 tập 1
- Giải câu 2 Trang 43 sách VNEN toán 8 tập 1











