Giải câu 5 trang 125 toán VNEN 8 tập 1

Câu 5: Trang 125 toán VNEN 8 tập 1

Cho tam giác đều ABC cạnh a và điểm M bất kì nằm trong tam giác đó. Gọi H, K, T tương ứng là hình chiếu vuông góc của điểm M trên BC, CA, AB.

Chứng minh rằng: MH + MK + MT = $\frac{a\sqrt{3}}{2}$ .

Bài làm:

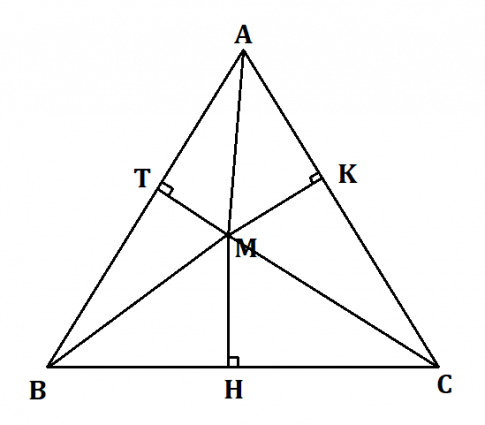
Từ A kẻ đường thẳng AD. Vì ABC là tam giác đều nên AD đồng thời là đường trung tuyến của tam giác ABC $\Rightarrow$ BD = $\frac{B C}{2}$ .

Theo định lí Pi-ta-go, ta có: AD = $\sqrt{AB^{2} - BD^{2}}$ = $\sqrt{a^{2} - (\frac{a}{2})^{2}}$ = $\frac{a \sqrt{3}}{2}$ .

Khi đó: S $_{ABC}$ = $\frac{A D . B C}{2}$ = $\frac{a . a \sqrt{3}}{4}$ = $\frac{a^{2} \sqrt{3}}{4}$ (1).

Mặt khác, ta có: S $_{ABC}$ = S $_{M A B}$ + S $_{M A C}$ + S $_{M B C}$ = $\frac{M T . A B}{2}$ + $\frac{M K . A C}{2}$ + $\frac{M H . B C}{2}$

$\Rightarrow$ S $_{A B C}$ = $\frac{a . (M K + M T + M H)}{2}$ (2).

Từ (1) và (2) $\Rightarrow$ $\frac{a . (M K + M T + M H)}{2}$ = $\frac{a^{2} \sqrt{3}}{4}$ hay MH + MK + MT = $\frac{a \sqrt{3}}{2}$ (đpcm).

Cập nhật: 07/09/2021

Xem thêm bài viết khác