Giải Câu 7 Bài 5: Khoảng cách

Câu 7: Trang 120 - SGK Hình học 11

Cho hình chóp tam giác đều có cạnh đáy bằng $3a$, cạnh bên bằng $2a$. Tính khoảng cách từ $S$ tới mặt đáy $(ABC)$.

Bài làm:

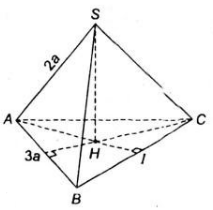
Gọi là trực tâm tam giác $ABC$.

Vì chóp S.ABC đều nên

=>

Gọi là trung điểm của $BC$.

Tam giác đều nên $AI=\frac{3a\sqrt{3}}{2}$

Áp dung định lí Pytago vào tam giác vuông ta có:

=>

Vậy khoảng cách từ đến mặt phẳng $(ABC)$ bằng $a$.