Giải câu 3 bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Câu 3: Trang 60 - SGK hình học 11

Cho tứ diện ABCD. Gọi M, N lần lượt là trung đểm của các cạnh AB, CD và G là trung điểm của đoạn MN

a) Tìm giao điểm A' của đường thẳng AG và mặt phẳng (BCD)

b) Qua M kẻ đường thẳng Mx song song với AA' và Mx cắt (BCD) tại M'. Chứng minh B, M', A' thẳng hàng và BM' = M'A' = A'N

c) Chứng minh GA = 3 GA'

Bài làm:

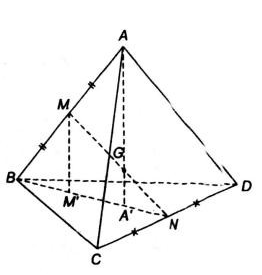
a) Trong mặt phẳng (ABN), gọi A’ = AG ∩ BN, ta có:

mà BN lại thuộc mặt phẳng (BCD)

=> A’ = AG ∩ (BCD)

b) *Chứng minh thẳng hàng

Từ M kẻ đường thẳng Mx song song với AA’.

Mx ⊂ (ABN) và Mx ∩ BN = M’

=>M' thuộc BN

=> B, M’,A’ thẳng hàng (đpcm)

*Chứng minh BM' = M'A' = A'N

MM’ là đường trung bình của tam giác ABA’ nên BM’ = M’A’ (1)

GA’ là đường trung bình của tam giác MM’N nên M’A’ = A’N (2)

=>

BN là đường trung tuyến và

=> A' là trọng tâm tam giác ∆BCD

=>BM’ = M’A’ = A’N (đpcm)

c) Áp dụng chứng minh câu b ta có:

∆ MM’N :2GA’=MM’

∆ BAA’:2 MM’=AA’

=>GA=3GA’.