Giải Câu 4 Bài Ôn tập cuối năm

Câu 4: Trang 126 - SGK Hình học 11

Cho hình lăng trụ tứ giác có $E,F,M$ và $N$ lần lượt là trung điểm của $AC,BD,A{C}^{\prime }$ và $B{D}^{\prime }$. Chứng minh $MN=EF$.

Bài làm:

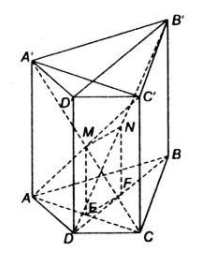
Vì là trung điểm của $A^{\prime }C$ và $E$ là trung điểm của $AC$ nên là đường trung bình trong $\mathrm{\Delta }A{A}^{\prime }C$

Tương tự ta có: là trung điểm của $B^{\prime }D$ và $F$ là trung điểm của $BD$ nên là đường trung bình trong $\mathrm{\Delta }B{B}^{\prime }D$

Ta lại có:

Từ (1), (2), (3) ⇒

=> tứ giác là hình bình hành, do đó $MN=EF$.