Giải Câu 9 Bài 1: Vecto trong không gian

Câu 9: Trang 92 - SGK Hình học 11

Cho tam giác . Lấy điểm $S$ nằm ngoài mặt phẳng $(ABC)$. Trên đoạn $SA$ lấy điểm $M$ sao cho $\overrightarrow{MS}$ = $-2\overrightarrow{MA}$ và trên đoạn $BC$ lấy điểm $N$ sao cho $\overrightarrow{NB}=-\frac{1}{2}\overrightarrow{NC}.$ Chứng minh rằng ba véctơ $\overrightarrow{AB}$, $\overrightarrow{MN}$, $\overrightarrow{SC}$ đồng phẳng.

Bài làm:

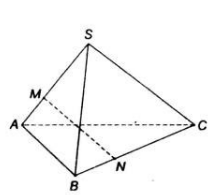
Theo đề bài: = $-2\overrightarrow{MA}$

=> và $\overrightarrow{MS}$ cùng hướng với $\overrightarrow{AS}$

=>

Lại có:

=> và $\overrightarrow{CN}$ cùng hướng với $\overrightarrow{CB}$

=>

Theo quy tắc chèn điểm, ta có:

= $\overrightarrow{MS}$ + $\overrightarrow{SC}$ + $\overrightarrow{CN}$

= + $\overrightarrow{SC}$ + $\frac{2}{3}\overrightarrow{CB}.$ (1)

= $\overrightarrow{MA}$ + $\overrightarrow{AB}$ + $\overrightarrow{BN}$

= + $\overrightarrow{AB}$ + $-\frac{1}{3}\overrightarrow{CB}.$ (2)

Nhân (2) với 2 rồi cộng với (1) ta được:

= $\overrightarrow{SC}$ + $2\overrightarrow{AB}$ $\iff \overrightarrow{MN}=\frac{1}{3}\overrightarrow{SC}+\frac{2}{3}\overrightarrow{AB}.$

Vậy , $\overrightarrow{MN}$, $\overrightarrow{SC}$ đồng phẳng.