Giải câu 2 bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

Câu 2: Trang 24 - sgk hình học 11

Cho hình chữ nhật ABCD. Gọi E, E, H, K, O, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, DA, KF, HC, KO. Chứng minh hai hình thang AEJK và FOIC bằng nhau.

Bài làm:

Hình vẽ như sau:

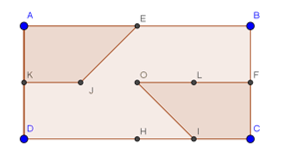
Gọi L là trung điểm của OF.

Ta thực hiện phép đối xứng của hình thang AEJK qua trục đối xứng EH thì A →B ; K → F; J → L => hình thang AEJK → hình thang BELF.

Ta thực hiện tiếp phép tính tiến hình thanh BELF thì B → F ; E → O; L → I; F → G => hình thang BELF → hình thang FOIC.

=>hai hình thang BELF và FOIC bằng nhau.