Giải Câu 3 Bài 1: Vecto trong không gian

Câu 3: Trang 91 - SGK Hình học 11

Cho hình bình hành . Gọi \(S\) là một điểm nằm ngoài mặt phẳng chứa hình bình hành. chứng minh rằng: \(\overrightarrow{SA}\) + \(\overrightarrow{SC}\) = \(\overrightarrow{SB}\) + \(\overrightarrow{SD}\).

Bài làm:

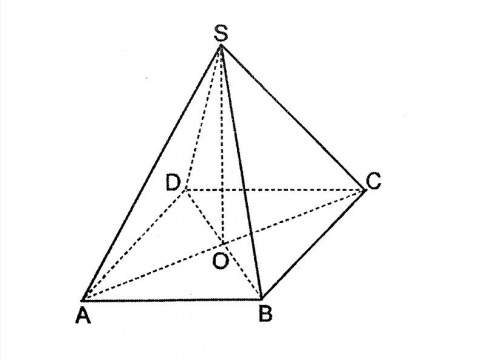
Gọi là tâm của hình bình hành \(ABCD\). Khi đó: là trung điểm của $AC,BD$

là trung tuyến của tam giác $SAC$

=> (quy tắc trung tuyến)

là trung tuyến của tam giác $SBD$

=> (quy tắc trung tuyến)

=>