Giải Câu 4 Bài: Bài tập ôn tập chương 3

Câu 4: Trang 121 - SGK Hình học 11

Hình chóp có đáy \(ABCD\) là hình thoi cạnh \(a\) và có góc \(\widehat{ BAD} = 60^0\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Đường thẳng SO vuông góc với mặt phẳng (ABCD) và \(SO = {{3a} \over 4}\) . Gọi \(E\) là trung điểm của đoạn \(BC\) và \(F\) là trung điểm của đoạn \(BE\).

a) Chứng minh mặt phẳng vuông góc với mặt phẳng \((SBC)\)

b) Tính các khoảng cách từ và \(A\) đến mặt phẳng \((SBC)\)

Bài làm:

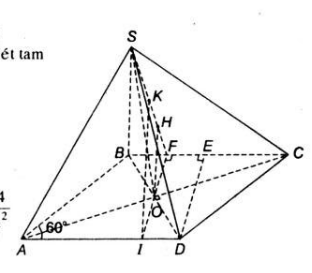
a) Theo giả thiết hình thoi có: => \(\widehat{ BCD} = 60^0\)

suy ra tam giác đều => hay \(\widehat{ OBC} = 60^0\)

là hình thoi => $AC\perp BD \equiv O$ => $\Delta BOC$ vuông tại O có $E$ là trung điểm $BC$

=> (tính chất đường trung tuyến ứng với cạnh huyền)

Xét tam giác có \(BO=BE-cmt\) và \(\widehat{ OBE} = 60^0\) nên tam giác đều

Có là trung điểm $BD$ => đồng thời là đường cao => \(OF ⊥BC\).

\(\left. \matrix{
SO \bot (ABCD) \hfill \cr
{\rm{OF}} \bot {\rm{BC}} \hfill \cr} \right\} \Rightarrow SF \bot BC\)

(Định lí 3 đường vuông góc)

\(\left. \matrix{
SF \bot BC \hfill \cr
{\rm{OF}} \bot {\rm{BC}} \hfill \cr} \right\} \Rightarrow BC \bot (SOF)\)

Mà

Suy ra

b) Vì và hai mặt phẳng này giao nhau theo giao tuyến \(SF\)

nên từ ta kẻ \(OH⊥SF\) => \(OH⊥(SBC)\) =>

Ta có:

\(\eqalign{
& SO = {{3a} \over 4}{\rm{;OF = }}{{a\sqrt 3 } \over 4} \Rightarrow SF = {{a\sqrt 3 } \over 2} \cr
& OH.SF = SO.{\rm{OF}} \Rightarrow {\rm{OH = }}{{3a} \over 8} \cr} \)

Gọi là hình chiếu vuông góc của \(A\) trên \((SBC)\), ta có \(AK//OH\)

Trong thì \(OH\) là đường trung bình, do đó: