Giải Bài 5: Khoảng cách

1 Đánh giá

Trong không gian, khoảng cách được tính như thế nào? Để biết chi tiết hơn, KhoaHoc xin chia sẻ với các bạn bài 5: Khoảng cách. Với kiến thức trọng tâm và các bài tập có lời giải chi tiết, hi vọng rằng đây sẽ là tài liệu giúp các bạn học tập tốt hơn.

A. TÓM TẮT KIẾN THỨC

1. Khoảng cách từ một điểm đến một mặt phẳng, đến một đường thẳng

Định nghĩa

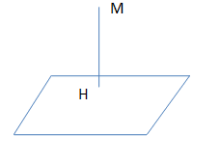
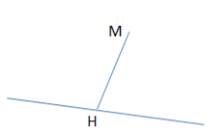
Khoảng cách từ 1 điểm M đến một mặt phẳng (P) (hoặc đến đường thẳng ∆) là khoảng cách giữa hai điểm M và H, trong đó H là hình chiếu của điểm M trên mặt phẳng (P), kí hiệu là d(M, (P)) (hoặc trên đường thẳng ∆, kí hiệu là d(M, ∆) .

Giải Bài 5: Khoảng cách-1 Giải Bài 5: Khoảng cách-2

2. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song

Định nghĩa

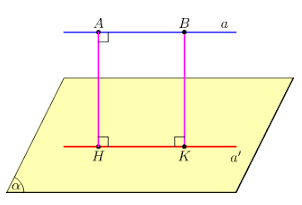
Khoảng cách giũa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì của a tới mặt phẳng (P) (h.3.57), kí hiệu là d(a, (P)).

Giải Bài 5: Khoảng cách=3

Định nghĩa

Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này tới mặt phẳng kia.

3. Khoảng cách giữa hai đường thẳng chéo nhau

Định nghĩa

Đường thẳng c cắt và vuông góc với cả a và b gọi là đường vuông góc chung của a và b.

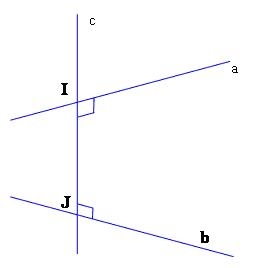
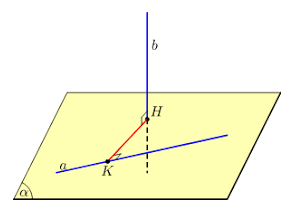
Giải Bài 5: Khoảng cách-5 Giải Bài 5: Khoảng cách-4

Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng chéo nhau đó.

Nhận xét

Khoảng cách giữa hai đường thẳng chéo nhau bằng:

Khoảng cách từ một trong hai đường thẳng đã cho đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
Khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó (h.3.59).

4. Cách xác định đường vuông góc chung của hai đường thẳng chéo nhau

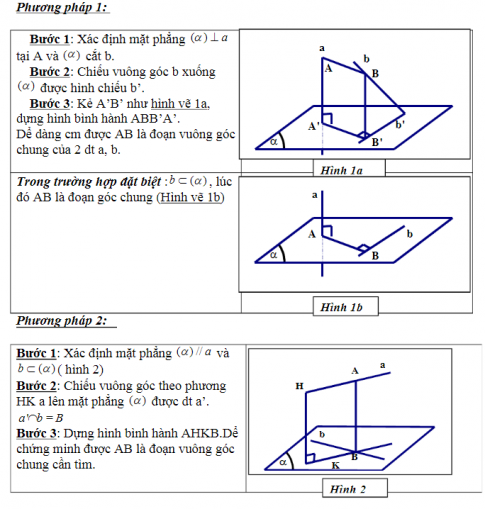
Giải Bài 5: Khoảng cách-6

B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI

Câu 1: Trang 119 - SGK Hình học 11

Trong các mệnh đề sau đây, mệnh đề nào đúng?

a) Đường thẳng $∆$ là đường thẳng vuông góc chung của hai đường thẳng $a$ và $b$ nếu $∆$ vuông góc với $a$ và $∆$ vuông góc với $b$ ;

b) Gọi $(P)$ là mặt phẳng song song với cả hai đường thẳng $a, b$ chéo nhau. Khi đó đường vuông góc chung $∆$ của $a$ và $b$ luôn luôn vuông góc với $(P)$ ;

c) Gọi $∆$ là đường vuông góc chung của hai đường thẳng chéo nhau $a$ và $b$ thì $∆$ là giao tuyến của hai mặt phẳng $(a, ∆)$ và $(b, ∆)$ ;

d) Cho hai đường thẳng chéo nhau $a$ và $b$ . Đường thẳng nào đi qua một điểm $M$ trên $a$ đồng thời cắt $b$ tại $N$ và vuông góc với $b$ thì đó là đường vuông góc chung của $a$ và $b$ ;

e) Đường vuông góc chung $∆$ của hai đường thẳng chéo nhau $a$ và $b$ nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.

=> Xem hướng dẫn giải

Câu 2: Trang 119 - SGK Hình học 11

Cho tứ diện $S.ABC$ có $S A$ vuông góc với mặt phẳng $(A B C)$ . Gọi $H, K$ lần lượt là trực tâm của tam giác $A B C$ và $S B C$ .

a) Chứng minh ba đường thẳng $AH, SK, BC$ đồng quy.

b) Chứng minh rằng $SC$ vuông góc với mặt phẳng $(B H K)$ và $H K$ vuông góc với mặt phẳng $(S B C)$ .

c) Xác định đường vuông góc chung của $BC$ và $S A$ .

=> Xem hướng dẫn giải

Câu 3: Trang 119 - SGK Hình học 11

Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$ . Chứng minh rằng các khoảng cách từ các điểm $B, C, D, A^{'}, B^{'}, D^{'}$ đến đường chéo $A C^{'}$ đều bằng nhau. Tính khoảng cách đó.

=> Xem hướng dẫn giải

Câu 4: Trang 119 - SGK Hình học 11

Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $A B = a, B C = b, C C^{'} = c$ .

a) Tính khoảng cách từ $B$ đến mặt phẳng $(A C C^{'} A^{'})$ .

b) Tính khoảng cách giữa hai đường thẳng $BB'$ và $A C^{'}$ .

=> Xem hướng dẫn giải

Câu 5: Trang 119 - SGK Hình học 11

Cho hình lập phương $ABCD.A'B'C'D'$ cạnh $a$ .

a) Chứng minh rằng $B'D$ vuông góc với mặt phẳng $(B A^{'} C^{'})$ .

b) Tính khoảng cách giữa hai mặt phẳng $(BA'C')$ và $(A C D^{'})$ .

c) Tính khoảng cách giữa hai đường thẳng $BC'$ và $C D^{'}$ .

=> Xem hướng dẫn giải

Câu 6: Trang 119 - SGK Hình học 11

Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh $AB$ và $C D$ của tứ diện $A B C D$ là đường vuông góc chung của $AB$ và $C D$ thì $A C = B D$ và $A D = B C$ .