Giải Câu 4 Bài 1: Vecto trong không gian

Câu 4: Trang 92 - SGK Hình học 11

Cho hình tứ diện . Gọi $M$ và $N$ lần lượt là trung điểm của $AB$ và $CD$. Chứng minh rằng:

a)

b)

Bài làm:

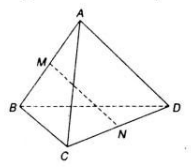
a)

Cộng từng vế ta được:

là trung điểm $AB$ nên: $\overrightarrow{MA}+\overrightarrow{MB}=0$

là trung điểm $CD$ nên: $\overrightarrow{DN}+\overrightarrow{CN}=0$

=>

=>

b) Tương tự câu a,ta có:

Cộng từng vế ta được:

là trung điểm $AB$ nên: $\overrightarrow{MA}+\overrightarrow{MB}=0$

là trung điểm $CD$ nên: $\overrightarrow{DN}+\overrightarrow{CN}=0$

=>

=>