Giải bài 4: Phép đối xứng tâm

Một phép biến hình quen thuộc nữa chúng ta đã được học là phép đối xứng tâm. Phép biến hình này làm cho một số tác phẩm nghệ thuật trở nên đặc biệt và thu hút hơn bao giờ hết.

A. Lí thuyết

1. Định nghĩa

Định nghĩa: Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác I thành M' sao cho I là trung điểm của đoạn thẳng MM' được gọi là phép đối xứng tâm I.

Điểm I được gọi là tâm đối xứng. Phép đối xứng tâm I thường được kí hiệu là .

Ví dụ:

2. Biểu thức tọa độ

Trong hệ trục tọa độ Oxy, cho điểm M(x,y) và khi đó $\{\begin{array}{c}{x}^{\prime }=-x\\ y^{\prime }=-y\end{array}$.

3. Tính chất

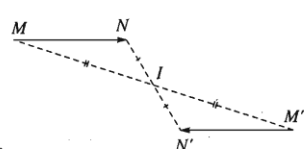
Tính chất 1: Nếu thì $\overrightarrow{M^{\prime }{N}^{\prime }}=-\overrightarrow{MN}$, từ đó suy ra $M^{\prime }{N}^{\prime }=MN$.

Tính chất 2: Phép đối xứng tâm biến

• đường thẳng thành đường thẳng song song hoặc trùng với nó,
• đoạn thẳng thành đoạn thẳng bằng nó,
• tam giác thành tam giác bằng nó,
• đường tròn thành đường tròn có cùng bán kính.

4. Tâm đối xứng của một hình

Định nghĩa: Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến H thành chính nó. Khi đó ta nói H là hình có tâm đối xứng.

Ví dụ: