Giải Bài 4: Hai mặt phẳng vuông góc
Khi nào hai mặt phẳng vuông góc với nhau? Dựa vào cấu trúc SGK, KhoaHoc sẽ tóm tắt kiến thức cần nhớ và hướng dẫn giải các bài tập một cách chi tiết, dễ hiểu cho bài học: "Hai mặt phẳng vuông góc". Hy vọng đây là tài liệu có ích với các em.
A. TÓM TẮT KIẾN THỨC
1. Góc giữa hai mặt phẳng
Định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
2. Hai mặt phẳng vuông góc
Định nghĩa
Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng 
Định lý: Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Hệ quả 1
Nếu hai mặt phẳng và \((Q)\) vuông góc với nhau thì bất cứ đường thẳng \(a\) nào nằm trong mặt phẳng , vuông góc với giao tuyến của và \((Q)\) đều vuông góc với mp \((Q)\).
Hệ quả 2
Nếu hai mặt phẳng và \((Q)\) vuông góc với nhau và \(A\) là một điểm nằm trong thì đường thẳng \(a\) đi qua điểm \(A\) và vuông góc với \((Q)\) sẽ nằm trong .
Hệ quả 3
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
3. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương
- Hình lăng trụ đứng là hình lăng trụ đứng có đáy là đa giác đều.
- Hình hộp đứng là hình lăng trụ đứng có đáy là hình bình hành.
- Hình hộp chữ nhật là hình hộp đứng có đấy là hình chữ nhật.
- Hình lập phương là hình hộp có tất cả các mặt là hình vuông.
4. Hình chóp đều và hình chóp cụt đều
Hình chóp đều
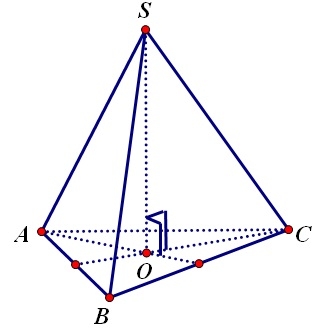
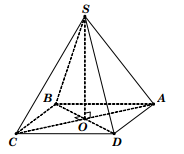
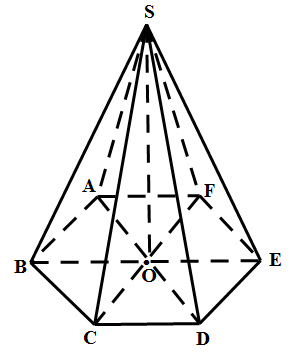
Một hình chóp được gọi là hình chóp đều nếu đáy của nó là 1 đa giác đều và đường cao của hình chóp đi qua tâm của đấy.
Hình chóp đều có các mặt cạnh bên tạo với mặt đáy các góc bằng nhau.
Hình chóp cụt đều
Phần của hình chóp đều nằm giữa đáy và một thiết diện song song với đáy gọi là hình chóp cụt đều.
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
Câu 1: Trang 113 - SGK Hình học 11
Cho ba mặt phẳng những mệnh đề nào sau đây đúng?
a) Nếu (α) ⊥ (β) và (α) // () thì (β) ⊥
b) Nếu (α) ⊥ (β) và (α) ⊥ thì (β) //
Câu 2: Trang 113 - SGK Hình học 11
Cho hai mặt phẳng và \((\beta)\) vuông góc với nhau. Người ta lấy trên giao tuyến \(\Delta\) của hai mặt phẳng đó hai điểm \(A\) và \(B\) sao cho \(AB=8cm\). Gọi \(C\) là một điểm trên và \(D\) là một điểm trên \((\beta)\) sao cho \(AC\) và \(BD\) cùng vuông góc với giao tuyến \(\Delta\) và \(AC=6cm\), \(BD=24cm\). Tính độ dài đoạn \(CD\).
Câu 3; Trang 113 - SGK Hình học 11
Trong mặt phẳng cho tam giác \(ABC\) vuông ở \(B\). Một đoạn thẳng \(AD\) vuông góc với tại \(A\). Chứng minh rằng:
a) là góc giữa hai mặt phẳng \((ABC)\) và \((DBC)\);
b) Mặt phẳng vuông góc với mặt phẳng \((BCD)\);
c) với \(H\) và \(K\) lần lượt là giao điểm của \(DB\) và \(DC\) với mặt phẳng \((P)\) đi qua \(A\) và vuông góc với \(DB\).
Câu 4: Trang 114 - SGK Hình học 11
Cho hai mặt phẳng , \((\beta)\) cắt nhau và một điểm \(M\) không thuộc và không thuộc \((\beta)\). Chứng minh rằng qua điểm \(M\) có một và chỉ một mặt phẳng \((P)\) vuông góc với và \((\beta)\). Nếu song song với \((\beta)\) thì kết quả trên sẽ thay đổi như thế nào?
Câu 5: Trang 114 - SGK Hình học 11
Cho hình lập phương . Chứng minh rằng:
a) Mặt phẳng vuông góc với mặt phẳng \((BCD'A')\);
b) Đường thẳng vuông góc với mặt phẳng \((A'BD)\).
Câu 6: Trang 114 - SGK Hình học 11
Cho hình chóp có đáy \(ABCD\) là một hình thoi cạnh \(a\) và có \(SA = SB = SC = a\). Chứng minh rằng:
a) Mặt phẳng vuông góc với mặt phẳng \((SBD)\);
b) Tam giác là tam giác vuông.
Câu 7: Trang 114 - SGK Hình học 11
Cho hình hộp chữ nhật có \(AB = a, BC = b, CC' = c\).
a) Chứng minh rằng mặt phẳng vuông góc với mặt phẳng \((ABB'A')\).
b) Tính độ dài đường chéo theo \(a, b, c\).
Câu 8: Trang 114 - SGK Hình học 11
Tính độ dài đường chéo của một hình lập phương cạnh .
Câu 9: Trang 114 - SGK Hình học 11
Cho hình chóp tam giác đều có \(SH\) là đường cao. Chứng minh \(SA ⊥ BC\) và \(SB ⊥ AC\)
Câu 10: Trang 114 - SGK Hình học 11
Cho hình chóp tứ giác đều có các cạnh bên và cạnh đáy đều bằng \(a\). Gọi \(O\) là tâm của hình vuông \( ABCD\).
a) Tính độ dài đoạn thẳng .
b) Gọi là trung điểm của đoạn \(SC\). Chứng minh hai mặt phẳng \((MBD)\) và \((SAC)\) vuông góc với nhau.
c) Tính độ dài đoạn và tính góc giữa hai mặt phẳng \((MBD)\) và \((ABCD)\).
Câu 11: Trang 114 - SGK Hình học 11
Cho hình chóp có đáy \(ABCD\) là một hình thoi tâm \(I\) cạnh \(a\) và có góc \(A\) bằng \(60^{0},\) cạnh \(SC=\frac{a\sqrt{6}}{2}\) và \(SC\) vuông góc với mặt phẳng \((ABCD)\).
a) Chứng minh mặt phẳng vuông góc với mặt phẳng \((SAC)\).
b) Trong tam giác kẻ \(IK\) vuông góc với tại $K$. Hãy tính độ dài
c) Chứng minh và từ đó suy ra mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((SAD)\).
Lớp 11