Giải Câu 10 Bài 4: Hai mặt phẳng vuông góc

1 Đánh giá

Câu 10: Trang 114 - SGK Hình học 11

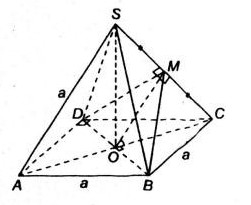
Cho hình chóp tứ giác đều $S.ABCD$ có các cạnh bên và cạnh đáy đều bằng $a$ . Gọi $O$ là tâm của hình vuông $A B C D$ .

a) Tính độ dài đoạn thẳng $SO$ .

b) Gọi $M$ là trung điểm của đoạn $S C$ . Chứng minh hai mặt phẳng $(M B D)$ và $(S A C)$ vuông góc với nhau.

c) Tính độ dài đoạn $OM$ và tính góc giữa hai mặt phẳng $(M B D)$ và $(A B C D)$ .

Bài làm:

Giải Câu 10 Bài 4: Hai mặt phẳng vuông góc

a) $ABCD$ là hình vuông cạnh $a$

=> tam giác ABC vuông tại B

=> $AC=\sqrt{AB^2+BC^2}=\sqrt{a^2+a^2}=a\sqrt{2}$

Lại có $O$ là tâm hình vuông $A B C D (g t)$ nên $O$ là trung điểm của $A C$

=> $OA=\frac{1}{2}.AC=a.\frac{\sqrt{2}}{2}$

Hình chóp tứ giác đều nên $SO\bot (ABCD)$ . Do đó $S O ⊥ A C$

Xét tam giác $SOA$ vuông tại $O$ : có $SA^2=OA^2+SO^2$ (định lý Pitago)

=> $SO = \sqrt{SA^{2}-AO^{2}}=\frac{a\sqrt{2}}{2}.$

b) $BD\bot AC$ (tính chất hình vuông) (1)

Vì $SO\perp (ABCD), BD\subset (ABCD)=>SO\perp BD$ (2)

Từ (1)(2) và $AC \cap SO$ suy ra: $BD \bot (SAC)$ ,

Mà $BD ⊂ (MBD)$ do đó $(M B D) ⊥ (S A C) (đ p c m)$ .

c) $\Delta SCD$ và $Δ S C B$ có:

$SC$ chung

$SD=SB(=a);CD=CB(=a)$

=> $\Delta SCD\sim \Delta SCB(c.c.c)$

=> $DM=BM$ (trung tuyến tương ứng của 2 tam giác bằng nhau)

suy ra $DM=BM$ suy ra tam giác $B D M$ cân tại $M$

=> $OM$ vừa là trung tuyến đồng thời là đường cao nên $O M ⊥ B D$

Ta có:

$\begin{matrix} (M B D) \cap (A B C D) = B D \\ O M ⊥ B D \\ O C ⊥ B D \end{matrix}}$

$\Rightarrow$ góc giữa hai mặt phẳng $(MBD)$ và $(A B C D)$ là $\hat{M O C}$

Trong $\Delta SOC$ vuông tại O có $O M$ là trung tuyến ứng với cạnh huyền $S C$

suy ra: $OM=MC=\frac{SC}{2}=\frac{a}{2}$ hay Tam giác $O M C$ vuông cân tại $M$

suy ra: $(\widehat{(MBD);(ABCD)})=(\widehat{MOC})=45^{0}.$

lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Toán Hình 11