Giải Câu 4 Bài 4: Hai mặt phẳng vuông góc

Câu 4: Trang 114 - SGK Hình học 11

Cho hai mặt phẳng , $(\beta )$ cắt nhau và một điểm $M$ không thuộc và không thuộc $(\beta )$. Chứng minh rằng qua điểm $M$ có một và chỉ một mặt phẳng $(P)$ vuông góc với và $(\beta )$. Nếu song song với $(\beta )$ thì kết quả trên sẽ thay đổi như thế nào?

Bài làm:

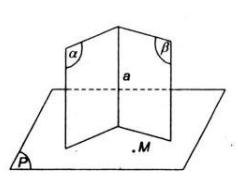
Điều kiện cần: Qua có một mặt phẳng $(P)$ vuông góc với và $(\beta )$

Gọi . Gọi $(P)$ là mặt phẳng đi qua $M$ và vuông góc với $a$.

Vì nên $(P)\mathrm{\perp }(\alpha )$, $a\subset (\beta )$ nên $(P)\mathrm{\perp }(\beta )$ (Tính chất: mặt phẳng vuông góc với giao tuyến của hai mặt phẳng thì vuông góc với từng mặt phẳng)

Như vậy qua có mặt phẳng $(P)$ vuông góc với $(\alpha )$ và $(\beta )$.

Điều kiện đủ: Mặt phẳng là duy nhất.

Nếu có đi qua $M$ và vuông góc với $(\alpha )$ và $(\beta )$ thì $(P)\mathrm{\perp }a$. Do tính duy nhất của mặt phẳng đi qua một điểm và vuông góc với một đường thẳng cho trước nên duy nhất.

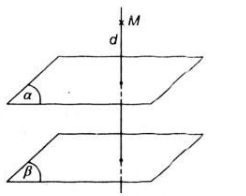
Nếu thì: gọi $d$ là đường thẳng đi qua $M$ và vuông góc với $(\alpha )$ khi đó ta có $d\mathrm{\perp }(\beta )$. Như vậy mọi mặt phẳng chứa $d$ đều vuông góc với $(\alpha )$ và $(\beta )$.

Do đó khi thì có vô số mặt phẳng $(P)$ đi qua $M$ và vuông góc với $(\alpha )$ và $(\beta )$.