Giải Câu 3 Bài Ôn tập cuối năm

Câu 3: Trang 125 - SGK Hình học 11

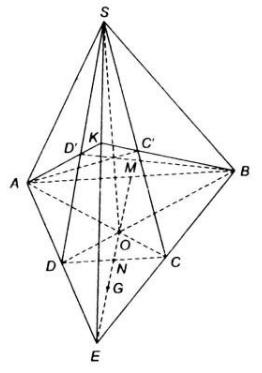
Cho hình chóp có đáy $ABCD$ là hình thang với $AB$ là đáy lớn. Gọi $M$ là trung điểm của đoạn $AB$, $E$ là giao điểm của hai cạnh của hình thang $ABCD$ và $G$ là trọng tâm của tam giác $ECD$.

a) Chứng minh rằng bốn điểm cùng thuộc một mặt phẳng $(\alpha )$ và mặt phẳng này cắt cả hai mặt phẳng $(SAC)$ và $(SBD)$ theo cùng một giao tuyến $d$.

b) Xác định giao tuyến của hai mặt phẳng và $(SBC)$.

c) Lấy một điểm trên đoạn $SE$ và gọi $C^{\prime }=SC\cap KB,D^{\prime }=SD\cap KA$. Chứng minh rằng hai giao điểm của $A{C}^{\prime }$ và $B{D}^{\prime }$ thuộc đường thẳng $d$ nói trên.

Bài làm:

a)

• Gọi là giao điểm của $AC$ và $DB$; $N$ là giao của $EM$ và $DC$.

là trung điểm của $AB$ => $N$ là trung điểm của $DC$ (vì $ABCD$ là hình thang),

=> là trung tuyến tròn tam giác

mà là trọng tâm $\mathrm{\Delta }ECD$

=> đi qua $G$ => $G\in EN$ mà $E,N,M$ thẳng hàng

nên ba điểm thẳng hàng

Gọi là mặt phẳng $(SEM)$

Vậy 4 điểm cùng thuộc mặt phẳng $(\alpha )$.

• $\Rightarrow O\in (\alpha )$ và $O\in AC\subset (SAC)$ nên $O$ là giao điểm của hai mặt phẳng $(\alpha )$ và $(SAC)$

là giao tuyến của $(\alpha )$ và $(SAC)$. (1)

• Tương tự ta có: $\Rightarrow O\in (\alpha )$ và $O\in BD\subset (SBD)$ nên $O$ là giao điểm của hai mặt phẳng $(\alpha )$ và $(SBD)$

là giao tuyến của $(\alpha )$ và $(SBD)$. (2)

Từ (1) (2) suy ra cắt hai mặt phẳng $(SAC)$ và $(SBD)$ theo cùng một giao tuyến $d\equiv SO$

b)

Vậy là một điểm chung của hai mặt phẳng $(SAD)$ và $(SBC)$

là điểm chung thứ hai của hai mặt phẳng $(SAD)$ và $(SBC)$

=> là giao tuyến của $(SAD)$ và $(SBC)$

c)

Tương tự ta có:

Mà hai đường thẳng và $B{D}^{\prime }$ cùng thuộc mặt phẳng $(ABK)$ và giao nhau tại điểm

=>

là điểm chung của hai mặt phẳng $(SAC)$ và $(SDB)$ hay $M\in d$