Giải câu 3 bài 4: Hai mặt phẳng song song

Câu 3: Trang 71 - SGK hình học 11

Cho hình hộp ABCD.A’B’C’D’.

a) chứng minh rằng hai mặt phẳng (BDA’) và (B’D’C) song song với nhau.

b) Chứng minh rằng đường chéo AC’ đi qua trọng tâm G1 và G2 lần lượt của hai tam giác BDA’ và B’D’C.

c) Chứng minh G1 và G2 chia đoạn AC’ thành ba phần bằng nhau.

d) Gọi O và I lần lượt là tâm các hình bình hành ABCD và ∆A’C’C. Xác định thiết diện của mặt phẳng (A’IO) với hình hộp đã cho.

Bài làm:

Theo giả thiết ta có hình vẽ sau:

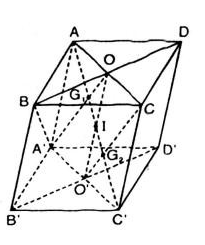
a) Do ABCDA'B'C'D' là hình hộp chữ nhật, ta có:

A’B // D’C và D’C ⊂ (B’D’C) => A’B // (B’D’C) (1)

BD // B’D’ và B’D’ ⊂ (B’D’C) => BD // (B’D’C) (2)

A’B ⊂ (BDA’) và BD ⊂ (BDA’) (3)

Từ (1), (2), (3) suy ra : (BDA’) // (B’D’C). (đpcm)

b) Gọi O là giao điểm của hai đường chéo AC, BD của hình bình bình hành ABCD => A’O ⊂ (A’ACC’).

Trong mặt phẳng (A’ACC’) hai đường thẳng A’O và AC’ cắt nhau tại điểm G₁, G₁ ∈ A’O và A’O ⊂ (BDA’)

=> G₁ ∈ (BDA’),G₁ ∈ AC’

Vậy G₁ ∈ AC’ ∩(BDA’)

Tứ giác ACC’A’ là hình bình hành, giao điểm I của hai đường chéo A’C và AC’ là trung điểm của mỗi đường.

Xét tam giác AA’C, các trung tuyến A’O và AI cắt nhau tại G₁. Vậy G₁ là trọng tâm của ∆AA’C cho ta OG₁/OA' = 1/3 , A’O cũng là trung tuyến của ∆BDA’ nên tỉ số OG₁/OA' = 1/3 chứng tỏ G1 là trọng tâm của tam giác BDA’.

Chứng minh tương tự đối với điểm G₂.

c) Vì G₁ là trọng tâm của ∆AA’C nên .

Vì I là trung điểm của AC’ nên

Từ các kết quả này, ta có :

Chứng minh tương tự ta có :

Suy ra : AG₁ = GG₂ = G₂C’ = .

d) Thiết diện của mặt phẳng (A'IO) với hình hộp chính là hình bình hành AA’C’C.