Giải Câu 9 Bài 4: Hai mặt phẳng vuông góc
Câu 9: Trang 114 - SGK Hình học 11
Cho hình chóp tam giác đều ![]() có \(SH\) là đường cao. Chứng minh \(SA ⊥ BC\) và \(SB ⊥ AC\)
có \(SH\) là đường cao. Chứng minh \(SA ⊥ BC\) và \(SB ⊥ AC\)
Bài làm:
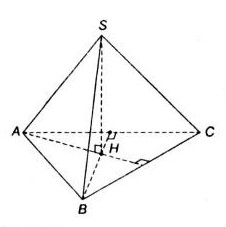
- Chứng minh

Vì ![]() là chóp đều có $SH$ là đường cao nên $SH\perp (ABC)$ tại $H$ là trực tâm của $\Delta ABC$
là chóp đều có $SH$ là đường cao nên $SH\perp (ABC)$ tại $H$ là trực tâm của $\Delta ABC$
![]() , $BC\subset (ABC)$ $\Rightarrow SH \perp BC$
, $BC\subset (ABC)$ $\Rightarrow SH \perp BC$
VÌ ![]() là trực tâm của $\Delta ABC$ nên $AH\perp BC$
là trực tâm của $\Delta ABC$ nên $AH\perp BC$
Ta có:

mà ![]()
![]()
- Chứng minh

Vì ![]() là trực tâm tam giác ABC nên $BH\perp AC$.
là trực tâm tam giác ABC nên $BH\perp AC$.
Lại có: ![]()
=> ![]() .
.
Ta có:

=> ![]()
Xem thêm bài viết khác
- Giải Bài 8: Phép đồng dạng
- Giải Câu 4 Bài Câu hỏi trắc nghiệm chương 3
- Giải Câu 6 Bài 2: Hai đường thẳng vuông góc
- Giải câu 5 bài 1: Đại cương về đường thẳng và mặt phẳng
- Giải Câu 3 Bài Ôn tập cuối năm
- Giải câu 2 bài 4: Hai mặt phẳng song song
- Giải Bài Ôn tập cuối năm
- Giải câu 3 bài 3: Đường thẳng và mặt phẳng song song
- Giải câu 6 bài 1: Đại cương về đường thẳng và mặt phẳng
- Giải Câu 3 Bài: Bài tập ôn tập chương 3
- Giải câu 1 bài 5: Phép quay
- Giải câu 3 bài 7: Phép vị tự











