Giải bài 3: Phép đối xứng trục

Từ THCS, ta đã biết đến khái niệm đối xứng trục. Bài học hôm nay ta cùng đi sâu và tìm hiểu kĩ hơn về đối xứng trục- một phép biến hình ứng dụng khá nhiều trong kiến trúc và hội họa.

A. Lí thuyết

1. Định nghĩa

Định nghĩa: Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.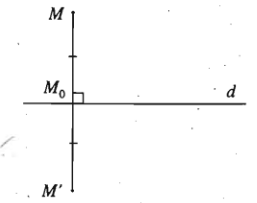

Ví dụ: Hình ảnh bàn cờ tướng

• Đường thẳng d được gọi là trục đối xứng.
• Phép đối xứng trục d kí hiệu là .

2. Biểu thức tọa độ

Chọn hệ trục tọa độ Oxy sao cho trục Ox trùng với đường thẳng d. Với mỗi điểm M(x,y) gọi thì $\{\begin{array}{c}{x}^{\prime }=x\\ y^{\prime }=-y\end{array}$

3. Tính chất

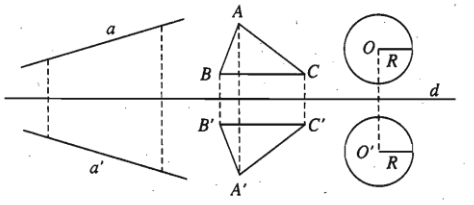
Tính chất 1: Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.

Tính chất 2: Phép đối xứng trục biến

• đường thẳng thành đường thẳng,
• đoạn thẳng thành đoạn thẳng bằng nó,
• tam giác thành tam giác bằng nó,
• đường tròn thành đường tròn có cùng bán kính.

4. Trục đối xứng của một hình

Định nghĩa: Đường thẳng d được gọi là trục đối xứng của hình H nếu phép đối xứng qua d biến H thành chính nó. Khi đó ta nói H là hình có trục đối xứng.

Ví dụ: