Giải Câu 6 Bài 3: Đường thẳng vuông góc với mặt phẳng

Câu 6: Trang 105 - SGK Hình học 11

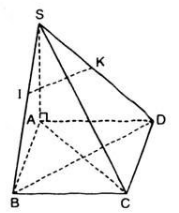
Cho hình chóp có đáy là hình thoi \(ABCD\) và có cạnh \(SA\) vuông góc với mặt phẳng \((ABCD)\). Gọi \(I\) và \(K\) là hai điểm lần lượt lấy trên hai cạnh \(SB\) và \(SD\) sao cho \(\frac{SI}{SB}=\frac{SK}{SD}.\) Chứng minh:

a) vuông góc với \(SC\);

b) vuông góc với mặt phẳng \((SAC)\).

Bài làm:

a) Ta có: (tính chất đường chéo hình thoi)

Lại có: (gt)

Ta có:

mà .

b) Theo giả thiết theo định lí ta lét ta có \(IK//BD\)

Từ chứng minh câu a, ta có: