Giải Câu 8 Bài 1: Vecto trong không gian

Câu 8: Trang 92 - SGK Hình học 11

Cho hình lăng trụ tam giác có \(\overrightarrow{AA'}\) = \(\overrightarrow{a}\), \(\overrightarrow{AB}\) = \(\overrightarrow{b}\), \(\overrightarrow{AC}\) = \(\overrightarrow{c}\). Hãy phân tích (hay biểu thị véctơ \(\overrightarrow{B'C}\), \(\overrightarrow{BC'}\) qua các véctơ \(\overrightarrow{a}\),\(\overrightarrow{b}\), \(\overrightarrow{c}\).

Bài làm:

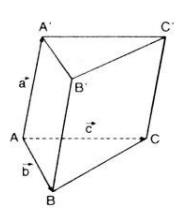
Theo quy tắc chèn điểm, ta có:

= \(\overrightarrow{B'A'}\) + \(\overrightarrow{A'A}\) + \(\overrightarrow{AC}\)

mà (gt); $\overrightarrow{B'A'}=-\overrightarrow{A'B'}=-\overrightarrow{AB}=-\overrightarrow{b}$

=> =\(-\overrightarrow{b}-\overrightarrow{a}+\overrightarrow{c}\).

Tương tự, ta có:

= \(\overrightarrow{BA}\) + \(\overrightarrow{AA'}\) + \(\overrightarrow{A'C'}\)

mà:

=> = \(-\overrightarrow{b} + \overrightarrow{a} + \overrightarrow{c}\).

Nhận xét: ba vectơ ; \(\overrightarrow{b}\); \(\overrightarrow{c}\) ở trên gọi là bộ ba vectơ cơ sở dùng để phân tích các vectơ khác.