Hướng dẫn giải bài 44- Đề thi thử THPT Quốc gia môn toán năm 2017 của Sở GD- ĐT Hồ Chí Minh- cụm chuyên môn VI

Câu 44: Cho số phức thỏa mãn $\sqrt{2}{z}_1=\sqrt{2}{z}_2=|z_1-z_2|=6\sqrt{2}$. Tính giá trị nhỏ nhất của biểu thức $P=|z|+|z-z_1|+|z-z_2|$.

A. .

B. .

C. .

D. .

Bài làm:

Gọi M, N, D lần lượt là điểm biểu diễn hai số phức trong mặt phẳng hệ tọa độ Oxy.

Gọi điểm E sao cho tam giác MNE là tam giác đều.

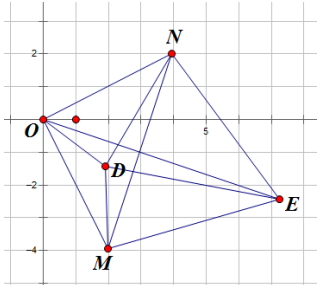
Từ giả thiết ta có .

Trong khi đó, bất đẳng thức Ptoleme khẳng định rằng với bốn điểm A, B, C, D bất kì trên mặt phẳng, ta có (2)

Áp dụng cho bốn điểm D,N, M, E ta có do MN=ME=NE nên ta có $MD+ND\ge DE$ như vậy $OD+MD+DN\ge OD+DE\ge OE$.

Hay