Lời giải bài số 21, 38, 41, 50 -Đề tham khảo số 7

1 Đánh giá

Bài làm:

Câu 21: Xét các số thực a, b thỏa mãn $\left\{\begin{matrix}a \geq b^{2}\\ b>1\end{matrix}\right.$ . Tìm giá trị nhỏ nhất của $P=\log_{\frac{a}{b}}a+\log_{b}\frac{a}{b}$.

A. $P_{\min}=\frac{1}{3}$ .

B. $P_{\min}=1$ .

C. $P_{\min}=3$ .

D. $P_{\min}=9$ .

Giải: Đáp án C.

Từ điều kiện $\left\{\begin{matrix}a>1\\ b>1\end{matrix}\right.$ .

Ta có $P=\frac{1}{1-\log_{a}b}+\frac{1-\log_{a}b}{\log_{a}b}$ .

Đặt $t= \log_{a}b>0$ . Do $a \geq b^{2} \Rightarrow \log_{b}a \geq \log_{b}b^{2}=2\Rightarrow t=\log_{a}b \leq \frac{1}{2}.$.

Khi đó $P=\frac{1}{1-t}+\frac{1-t}{t}=f(t)$ .

Khảo sát hàm số f(t) trên $(0,\frac{1}{2}]$ ta được $P=f(t) \geq f(\frac{1}{2})=3$.

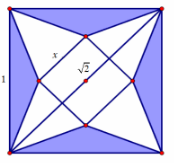Câu 38: Người ta cắt một tờ giấy hình vuông cạnh 1 để gấp thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp (hình vẽ). Để thể tích khối chóp lớn nhất thì cạnh đáy x của hình chóp bằng:

A. $x=\frac{\sqrt{2}}{5}$ .

B. $x=\frac{2 \sqrt{2}}{5}$ .

C. $x=2 \sqrt{2}$ .

D. $x= \frac{2}{5}$ .

Giải: Đáp án B

Ta có $BM=\frac{1}{2}AB-MO=\frac{\sqrt{2}}{2}-\frac{x}{2}$ .

Chiều cao của hình chóp:

$h=\sqrt{BM^{2}-MO^{2}}=\sqrt{(\frac{\sqrt{2}}{2}-\frac{x}{2})^{2}-(\frac{x}{2})^{2}}=\sqrt{\frac{1-x\sqrt{2}}{2}}$ .

Thể tích khối chóp $V=\frac{1}{3}x^{2}\sqrt{\frac{1-x\sqrt{2}}{2}}=\frac{1}{3}\sqrt{\frac{x^{4}-x^{5}\sqrt{2}}{2}}$ .

Khảo sát hàm số $f(x)=x^{4}-x^{5}\sqrt{2}$ trên $(0,\frac{\sqrt{2}}{2})$ ta được GTLN của hàm số đạt tại $x=\frac{2 \sqrt{2}}{5}$.
Cách 2: Giải theo trắc nghiệm: Ta loại đáp án C do $x=2 \sqrt{2}\notin (0,\frac{\sqrt{2}}{2})$ . Thay ba đáp án còn lại vào hàm số $f(x)=x^{4}-x^{5}\sqrt{2}$. So sánh kết quả nào lớn nhất ta chọn.

Câu 41: Một chiếc ly hình trụ có chiều cao bằng đường kính quả bóng bàn. Người ta đặt quả bóng lên trên miệng chiếc ly thấy phần ở ngoài của quả bóng có chiều cao bằng $\frac{3}{4}$ chiều cao của chiếc ly. Gọi $V_{1}, V_{2}$ lần lượt là thể tích của uqar bóng và chiếc ly, khi đó:

A. $9V_{1}=8V_{2}$ .

B. $3V_{1}=2V_{2}$ .

C. $16V_{1}=9V_{2}$ .

D. $8V_{1}=9V_{2}$ .

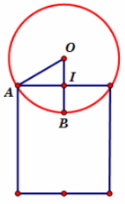Giải: Đáp án A.

Gọi h, R là chiều cao và bán kính của chiếc ly, r là bán kính của quả bóng.

Theo bài ra ta có $h=2r \Rightarrow r=OA=OB=\frac{h}{2}$

$IB=\frac{h}{4} \Rightarrow OI=\frac{h}{4}$ (do phần bên ngoài bằng $\frac{3}{4}h$).

Suy ra $R=IA=\sqrt{OA^{2}-OI^{2}}=\frac{h \sqrt{3}}{4}$ .

Do đó tỷ số thể tích $\frac{V_{1}}{V_{2}}=\frac{\frac{4}{3}\pi r^{3}}{\pi R^{2}h}=\frac{\frac{4}{3}\pi(\frac{h}{2})^{2}}{\pi (\frac{h\sqrt{3}}{4})^{2}h}=\frac{8}{9}$ .

Vậy $9V_{1}=8V_{2}$ .

Câu 50: Trong không gian với hệ tọa độ Oxyz, cho điểm E(8,1,1). Viết phương trình mặt phẳng $(\alpha)$ qua E và cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho OG nhỏ nhất với G là trọng tâm của tam giác ABC.

A. 2x+y+z-18=0.

B. 8x+y+z-66=0.

C. x+y+2z-11=0.

D. x+2y+2z-12=0.

Giải: Đáp án D.

Giả sử $(\alpha)$ cắt các tia Ox, Oy, Oz lần lượt tại A(a,0,0), B(0,b,0), C(0,0,c). Suy ra phương trình $(\alpha): \frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$. Lại có $E \in (\alpha)$ ta có $\frac{8}{a}+\frac{1}{b}+\frac{1}{c}=1$.

Trọng tâm tam gaisc ABc là $G(\frac{a}{3}, \frac{b}{3}, \frac{c}{3}) \Rightarrow 9 OG^{2}=a^{2}+b^{2}+c^{2}$ .

Bài toán trở thành " Cho x, y, z>0 thỏa mãn 8x+y+z=1. Tìm giá trị nhỏ nhất của $P=\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{1}{z^{2}}$ ".

Từ $\left\{\begin{matrix} x, y, z>0\\8x+y+z=1 \end{matrix}\right. \Rightarrow y+z=1-8x>0\Rightarrow x< \frac{1}{8}$ .

Ta có $P \geq \frac{1}{x^{2}}+\frac{2}{yz}\geq \frac{1}{x^{2}}+\frac{8}{(y+z)^{2}}=\frac{1}{x^{2}}+\frac{8}{(1-8x)^{2}}$ .

Khảo sát hàm số $f(x)=\frac{1}{x^{2}}+\frac{8}{(1-8x)^{2}}$ . trên $(0, \frac{1}{8})$, ta được $\min f(x)=f(\frac{1}{12})$.

Khi đó $y=z=\frac{1}{6}$ . Suy ra a=12, b=6, c=6. Vậy $(\alpha): x+2y+2z-12=0$.

2 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Tuyển tập đề thi THPT quốc gia môn Toán