Lời giải câu 27, 38, 49 đề thi thử THPT Quốc gia môn toán- Đề tham khảo số 2
Bài làm:
Câu 27: Tính tích phân  .
.
A. I=3.
B. I=1.
C. I=0.
D. I=2.
Giải: Đáp án C.
![]()
Tính ![]() .
.
Vậy ![]() .
.
Câu 38: Cho khối chóp S. ABCD có thể tích V và đáy là hình bình hành. gọi M là trung điểm của cạnh SA, N là điểm nằm trên cạnh SB sao cho SN=2 NB, mặt phẳng ![]() di động đi qua các điểm M, N và cắt các cạnh SC, CD lần lượt tại hai điểm phân biệt K, Q. Tính giá trị lớn nhất của thể tích khối chóp S.MNKQ.
di động đi qua các điểm M, N và cắt các cạnh SC, CD lần lượt tại hai điểm phân biệt K, Q. Tính giá trị lớn nhất của thể tích khối chóp S.MNKQ.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Giải: Đáp án B.
Gọi ![]()
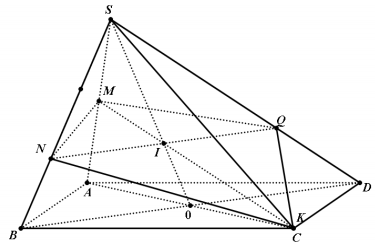
Vì mặt phẳng ![]() di động đi qua các điểm M, N và cắt các cạnh SC, SD lần lượt tại hai điểm phân biệt K, Q nên ta có:
di động đi qua các điểm M, N và cắt các cạnh SC, SD lần lượt tại hai điểm phân biệt K, Q nên ta có:
![]() $\Leftrightarrow \frac{SD}{SQ}=\frac{a+2}{2a}\Leftrightarrow \frac{SQ}{SD}=\frac{2a}{a+2}$.
$\Leftrightarrow \frac{SD}{SQ}=\frac{a+2}{2a}\Leftrightarrow \frac{SQ}{SD}=\frac{2a}{a+2}$.
![]() .
.
Xét hàm ![]() . Ta có
. Ta có
![]()
Suy ra giá trị lớn nhất của hàm f(x) là ![]()
Vậy giá trị lớn nhất của thể tích khối chóp ![]() là $V_{SMNKQ}=\frac{1}{2}.\frac{2}{3} V_{SABCD}=\frac{1}{3}V$.
là $V_{SMNKQ}=\frac{1}{2}.\frac{2}{3} V_{SABCD}=\frac{1}{3}V$.
Câu 49: Cho ba điểm A, B, C lần lượt nằm trên ba trục tọa độ Ox, Oy, Oz ( các điểm này không trùng với gốc tọa độ) thỏa mãn ![]() . Gọi I là tâm mặt cầu ngoại tiếp tứ diện OABC. Biết rằng khi A, B, C di chuyển thì điểm I nằm trên một mặt cầu cố định. Tính bán kính R của mặt cầu đó?
. Gọi I là tâm mặt cầu ngoại tiếp tứ diện OABC. Biết rằng khi A, B, C di chuyển thì điểm I nằm trên một mặt cầu cố định. Tính bán kính R của mặt cầu đó?
A. R=1.
B. R=2.
C. ![]() .
.
D. ![]() .
.
Giải: Đáp án A.
Gọi A(a,0,0), B(0,b,0), C(0,0,c) ![]() .
.
Ta có ![]() .
.
Từ ![]() .
.
Tính ![]() .
.
Vậy I luôn nằm trên mặt cầu tâm O có bán kính bằng 1.
Xem thêm bài viết khác
- Đề và đáp án môn Toán mã đề 113 thi THPT quốc gia năm 2017 đáp án của bộ GD-ĐT
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 114
- Thi THPTQG 2019: Đề thi và đáp án môn Toán mã đề 114
- Đề thi thử THPT quốc gia môn toán năm 2017 của trường THPT Hà Huy Tập lần 1
- Đáp án Đề thi thử THPT Quốc gia môn Toán năm 2017- Sở giáo dục và đào tạo tỉnh Hải Phòng
- Đáp án Đề thi thử THPT quốc gia môn toán năm 2017 của trường THPT Đông Sơn
- Đáp án Đề thi thử THPT quốc gia môn toán năm 2017 của Sở GD và ĐT Bắc Giang
- Thi THPTQG 2019: Đề thi và đáp án môn Toán mã đề 116
- Đáp án đề thi thử THPT quốc gia môn toán năm 2017- đề tham khảo số 10
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 121
- Thi THPTQG 2020: Đề thi và đáp án môn Toán mã đề 102
- Thi THPTQG 2019: Đề thi và đáp án môn Toán mã đề 110











