Toán 10: Đề kiểm tra học kì 2 dạng trắc nghiệm (Đề 6)

1 Đánh giá

Bài có đáp án. Đề kiểm tra học kì 2 dạng trắc nghiệm (Đề 6). Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.

Câu 1: Đường thẳng nào sau đây cách đều ba điểm A(4;1), B(6;11), C(2;9)?

A. x – 2y + 7 = 0
B. x + 2y + 1 = 0
C. 3x – 2y – 4 = 0
D. 5x – y – 8 = 0

Câu 2:Tính tổng tất cả các giá trị tham số m để hệ bất phương trình $\left\{\begin{matrix}x^{2} + 6x + 7 + m \leq 0\\ x^{2} + 4x + 7 - 4m \leq 0\end{matrix}\right.$ có nghiệm là một đoạn [a;b] trên trục số có độ dài bằng 1.

A. 4
B. $\frac{11}{4}$
C. $\frac{9}{2}$
D. $\frac{13}{3}$

Câu 3: Viết phương trình đường thẳng đi qua điểm M(1; –1) và cắt các đường thẳng x + y + 1 = 0, 2x – y – 1 = 0 tương ứng tại A, B sao cho $2\vec{MA} + \vec{MB} = \vec{0}$

A. x = y + 2
B. x = 1
C. x = 2y + 3
D. 3x = y + 4

Câu 4: Trong tam giác ABC, tính độ dài cạnh BC khi bcosC + ccosB = 8.

A. BC = 4
B. BC = 6
C. BC = 8
D. BC = 2 $\sqrt{2}$

Câu 5: Tồn tại bao nhiêu số nguyên m trong khoảng (–7; 7) để $x^{2} + y^{2}$ + 4mx - 2my + 2m + 3 = 0 là phương trình một đường tròn?

A. 13 số
B. 12 số
C. 11 số
D. 10 số

Câu 6: Tam giác ABC có BC = a, AC = b. Tìm số đo góc C để tam giác ABC có diện tích lớn nhất.

A. $60^{\circ}$
B. $120^{\circ}$
C. $45^{\circ}$
D. $90^{\circ}$

Câu 7: Tìm điều kiện tham số m để bất phương trình $x^{2} - 4x + 3 \geq m$ nghiệm đúng với mọi x thuộc đoạn [0;3].

A. $m \geq 2$
B. $\frac{7}{4} \leq m \leq 2$
C. $m \leq 1$
D. $m \geq 3$

Câu 8: Giả sử biểu thức P = 3sin2x - $4sin^{3}2x$ + 2cos6x có giá trị lớn nhất và giá trị nhỏ nhất tương ứng là M và m. Tính M – m.

A. 4
B. 2 $\sqrt{5}$
C. 6 $\sqrt{5}$
D. 8 $\sqrt{5}$

Câu 9: Tìm điều kiện tham số m để bất phương trình ( $m^{3}$ + 9m - 10)x + m - 4 < 0 có tập nghiệm S = R.

A. m = 4
B. m = –4
C. m = 1
D. m = 1

Câu 10: Tìm điều kiện tham số m để bất phương trình $\frac{x^{2} - 2x - 3m + 4}{3 - x +\sqrt{2-x}} > 0$ có nghiệm

A. m > 2
B. m < 1
C. m < 4
D. 2 < m < 4

Câu 11: Tìm tâm sai e của elip (E) biết nó có độ dài trục lớn bằng 4 và tiêu cực bằng 2 $\sqrt{2}$ .

A. e = 0,5
B. e = $\frac{\sqrt{2}}{2}$
C. e = $\frac{\sqrt{3}}{4}$
D. e = $\frac{\sqrt{5}}{5}$

Câu 12: Giả sử (a - 3b + 2)x + $a^{2}$ - 3b + 2 > 0, $\forall x\in R$. Mệnh đề nào sau đây có thể sai?

A. a + b > 2
B. a + b < $\frac{2}{3}$
C. 2a + b > 3
D. $\frac{3}{4}$ < a + b < 1

Câu 13: Tính điều kiện của tham số m để đường thẳng y = x + m cắt đường tròn $x^{2} + y^{2} = 2$ tại hai điểm phân biệt

A. |m| < $\sqrt{2}$
B. |m| < 3
C. |m| < 2
D. |m| < $\frac{4}{3}$

Câu 14: Biết $sin^{2}2x + 2sin^{2}\left ( x+\frac{\pi }{4} \right ) - 4sin2x + 2cos^{2}2x + 5 = asin^{2}2x + bsin2x + c$ . Tính a + b + c.

A. 6
B. 9
C. 10
D. 4

Câu 15: Tìm điều kiện tham số m để bất phương trình $2x^{2} - 3x + 1\geq m$ có nghiệm x thuộc đoạn [0; 2]

A. $\frac{-1}{8} \leq m \leq 1$
B. $1 \leq m \leq 3$
C. $m \leq 3$
D. $m \geq \frac{-1}{8}$

Câu 16: Tam giác ABC có R.sinB.sinC = 4 và a = 6. Tính diện tích S của tam giác ABC.

A. S = 36
B. S = 16
C. S = 12
D. S = 24

Câu 17: Cho hai điểm A (2;4), B (6;8). Đường trung trực d của đoạn thẳng AB đi qua điểm nào sau đây ?

A. (6; 4)
B. (2; 9)
C. (1; 0)
D. (4; -3)

Câu 18: Ký hiệu S là tập hợp nghiệm của bất phương trình $x^{2} - (m^{2} - 2m + 7)x + m^{2} - 2m + 6 \leq 0$ . Giả sử L là độ dài đoạn thẳng miền nghiệm trên trục số. Tìm giá trị tham số để L ngắn nhất.

A. m = 2
B. m = 0
C. m = 1
D. m = – 2

Câu 19: Gọi Q là điểm đối xứng của điểm P (2;0) qua đường thẳng $\left\{\begin{matrix}x = 1 + 3t\\ y = 2 + 4t\end{matrix}\right.$ . Tính độ dài đoạn thẳng PQ.

A. PQ = 6
B. PQ = 4
C. PQ = 7
D. PQ = $\sqrt{11}$

Câu 20: Cho hai góc lượng giác x, y thỏa mãn các điều kiện 4sinxsiny = 1; 4cosxcosy = 3$. Tính giá trị của biểu thức S = 5cos(x-y) + 6cos(x+y) + 7.

A. 18
B. 20
C. 15
D. 10

Câu 21: Tam giác ABC có b = 7, c = 5 và cosA = 0,6. Tính diện tích S của tam giác ABC.

A. S = 18
B. S = 12
C. S = 14
D. S = 20

Câu 22: Tìm điều kiện tham số m sao cho hệ bất phương trình $\left\{\begin{matrix}m^{2} - mx > 3(3-x)\\ 4x + 5 < 11 - x\end{matrix}\right.$ vô nghiệm.

A. $m \geq 3$
B. $m \geq -\frac{9}{5}$
C. $m \geq -\frac{1}{6}$
D. $m \geq -\frac{13}{2}$

Câu 23: Trong mặt phẳng với hệ tọa độ Oxy cho hình chữ nhật ABCD có đỉnh D (7;– 3) và cạnh BC thỏa mãn BC = 2AB. Gọi M, N lần lượt là trung điểm của AB và BC. Biết phương trình đường thẳng MN là x + 3y = 16, tỉnh tổng các tung độ có thể xảy ra đối với đỉnh C.

A. $\frac{31}{4}$
B. $\frac{6}{5}$
C. $\frac{11}{4}$
D. $\frac{9}{2}$

Câu 24: Một gia đình cần ít nhất 900 đơn vị Protein và 400 đơn vị (đv) Lipit trong định lượng thức ăn mỗi ngày. Một kg thịt bò chứa 800 đv Protein và 200 đv Lipit, một kg thịt lợn chứa 600 đv Protein và 400 đv Lipit. Hỏi mỗi ngày gia đình đó cần mua bao nhiêu kg thịt mỗi loại để chi phí rẻ nhất. Biết rằng mỗi ngày gia đình này chỉ mua không quá 1,6 kg thịt bò, không quá 1,1 kg thịt lợn. Và giá 1 kg thịt bò là 200 ngàn đồng, 1 kg thịt lợn là 100 ngàn đồng. Tính chi phí ít nhất gia đình đó có thể mua mà vẫn đảm bảo yêu cầu.

A. 60,5 ngàn đồng
B. 51,5 ngàn đồng
C. 40,5 ngàn đồng
D. 36 ngàn đồng

Câu 25: Tìm độ dài trục lớn elip (E) biết một tiêu điểm là (3;0) và một đường chuẩn x = 5.

A. $2\sqrt{15}$
B. 4
C. $2\sqrt{11$
D. $4\sqrt{2}$

Câu 26: Với các góc x, y, z, tồn tại bao nhiêu giá trị nguyên m thỏa mãn $\sqrt{sin(x+y+z) + 4} = m?

A. 4 giá trị
B. 3 giá trị
C. 2 giá trị
D. 1 giá trị

Câu 27: Cho hai góc x, y thỏa mãn tanx + tany = $\frac{2}{\sqrt{3}}$ ; cotx + coty =$ -\frac{2}{\sqrt{3}}$. Biểu thức tanx+ 6tany có thể nhận giá trị nào sau đây ?

A. 3
B. -2 $\sqrt{3}$
C. $-\sqrt{3}$
D. $\sqrt{2}$

Câu 28: Giả sử e là tâm sai của elip $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ . Mệnh đề nào sau đây đúng?

A. e > 1
B. $\frac{1}{2} < e < \frac{6}{7}$
C. $\frac{4}{5} < e < \frac{9}{10}$
D. $e < \sqrt{\frac{3}{17}}$

Câu 29: Tìm số nghiệm nguyên trong khoảng (– 19;19) của bất phương trình $(x^{2} - 14x + 48)\sqrt{x^{2} - 8x + 7} \geq 0$

A. 34 nghiệm
B. 37 nghiệm
C. 27 nghiệm
D. 36 nghiệm

Câu 30: Tồn tại bao nhiêu số nguyên m nhỏ hơn 3 để hàm số y = $\sqrt{\frac{x^{4} - x + 2}{5x^{2} - m + m}}$ xác định trên tập số thực ?

A. 1 giá trị
B. 2 giá trị
C. 4 giá trị
D. 5 giá trị

Câu 31: Tính chu vi p 11111111của hình chữ nhật cơ sở bao quanh elip $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$

A. p = 26
B. p = 32
C. p = 20
D. p = 1

Câu 32: Tìm điều kiện tham số m để hệ bất phương trình $\left\{\begin{matrix}x^{2} - 5x < 0\\ x^{2} - (m+4)x + 4m \leq 0\end{matrix}\right.$ có nghiệm.

A. m < 4
B. Mọi giá trị m.
C. m > 2
D. 0 < m < 4

Câu 33: Tập hợp các điểm M (x;y) thỏa mãn x = 3cosx; y = 2sinx là một elip (E)). Tính diện tích hình chữ nhật cơ sở bao quanh (E).

A. 20
B. 30
C. 24
D. 16

Câu 34: Tìm điều kiện tham số m để bất phương trình $\sqrt{4 - x}[(m^{2} + 1)x - 5m] \geq 0$ có tập nghiệm là [2; 4].

A. $m \in {2; \frac{1}{2}}$
B. m = 3
C. m = 2
D. $m \in {2; \frac{1}{2}; 0}$

Câu 35: Đường tròn (C) có tâm I (3;1) và cắt đường thẳng x – 2y + 4 = 0 theo một dây cung có độ dài bằng 4. Tìm bán kính R của (C).

A. R = 2
B. R = $\sqrt{3}$
C. R = 3
D. R = $\sqrt{6}$

Câu 36: Khoảng cách từ điểm A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc $52^{\circ}{16}'$ . Biết CA = 200m, BC = 180m. Khoảng cách AB gần nhất với giá trị nào ?

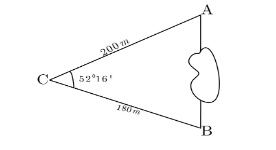
A. 163m
B. 224m
C. 112m
D. 168m

Câu 37: Tìm điều kiện của tham số m để bất phương trình ( $m^{2}$ - m + 1)x > 3m + 1 có tập nghiệm chứa miền (4; 5)

A. $m \geq 1$ hoặc $m \leq \frac{3}{4}$
B. $m \geq 4$ hoặc $m \leq \frac{3}{4}$
C. m > 3 hoặc $m < \frac{1}{4}$
D. m > 2 hoặc $m < \frac{1}{2}$

Câu 38: Hai đường thẳng $d_{1}$ : 3x + y - 6 = 0 và $d_{2}$: 2x - y + 5 = 0 cắt nhau tại M. Xét điểm N thuộc $d_{1}$ và P thuộc $d_{2}$ sao cho NP = 2. Tính $MN^{2} + MP^{2} - \sqrt{2}MN.MP$

A. 5
B. 4
C. 9
D. 2

Câu 39: Cho (x; y) thỏa mãn hệ bất phương trình $\left\{\begin{matrix}3x + y \leq 9\\ 2x + y \leq 8\\ x>0, y>0\end{matrix}\right.$

Giá trị lớn nhất của biểu thức Q = 4x + 3y.

A. 18
B. 20
C. 17
D. 31

Câu 40: Cho hai số thực dương x, y thay đổi sao cho x + y $\geq$ 6. Tìm giá trị nhỏ nhất của biểu thức P = 5x + 3y + $\frac{12}{x} + \frac{16}{y}$

A. 24
B. 40
C. 18
D. 32

Câu 41: Viết phương trình chính tắc của elip (E) khi nó có một đỉnh A, hai tiêu điểm $F_{1}; F_{2}$ tạo thành tam giác đều $AF_{1}F_{2}$, đồng thời chu vi hình chữ nhật cơ sở là 12(2+$\sqrt{3}$).

A. $\frac{x^{2}}{25} + \frac{y^{2}}{36} = 1$
B. $\frac{x^{2}}{36} + \frac{y^{2}}{27} = 1$
C. $\frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$
D. $\frac{x^{2}}{36} + \frac{y^{2}}{25} = 1$

Câu 42: Tồn tại bao nhiêu số nguyên a để hệ $\left\{\begin{matrix}x^{2} + y^{2} + 16 = 8x + 6y\\ 4x + 3y \leq a\end{matrix}\right.$ có nghiệm thực

A. 32 số
B. 25 số
C. 46 số
D. 31 số

Câu 43: Tìm giá trị lớn nhất của tham số m để bất phương trình $x(x-3)(x-5)(x-8) \geq m$ nghiệm đúng với mọi số thực x.

A. m = -4
B. m = $-\frac{225}{4}$
C. m = $\frac{-25}{4}$
D. m = $-\frac{123}{4}$

Câu 44: Trong mặt phẳng tọa độ Oxy, cho hình thoi ABCD có A nằm trên trục hoành, AC = 2BD và đường tròn tiếp xúc với các cạnh hình thoi có phương trình $x^{2} + y^{2} = 4$ . Viết phương trình chính tắc của elip (E) đi qua các đỉnh của hình thoi.

A. $\frac{x^{2}}{20} + \frac{y^{2}}{5} = 1$
B. $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$
C. $\frac{x^{2}}{64} + \frac{y^{2}}{25} = 1$
D. $\frac{x^{2}}{8} + \frac{y^{2}}{4} = 1$

Câu 45: Giả sử $(x_{1}; y_{1}), (x_{1}; y_{1})$ là hai nghiệm của hệ $\left\{\begin{matrix}x + my - m = 0\\ x^{2} + y^{2} - x = 0\end{matrix}\right.$

Tìm giá trị lớn nhất của biểu thức M = $(x_{1}- x_{2})^{2} + (y_{1}; y_{2})^{2}$

A. 1
B. 2
C. 0,5
D. 2

Câu 46: Đường tròn (C): $x^{2} + y^{2} - ax + by - c = 0$ đi qua hai điểm A (2; 3), B (–1; 1) và có tâm I nằm trên đường thẳng x = 3y + 11. Tính giá trị biểu thức M = a + b + c.

A. M = 10
B. M = 30
C. M = 14
D. M = 26

Câu 47: Trong mặt phẳng tọa độ Oxy, elip (E) đi qua M(- $\sqrt{3}$ ; 1)và khoảng cách giữa hai đường chuẩn của (E) bằng 6. Viết phương trình chính tắc của (E).

A. $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$
B. $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$
C. $\frac{x^{2}}{64} + \frac{y^{2}}{36} = 1$
D. $\frac{x^{2}}{6} + \frac{y^{2}}{2} = 1$

Câu 48: Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm cạnh AB, N là điểm thuộc cạnh AC sao cho 4CN = AC. Giả sử E (1; -1) là trung điểm của đoạn DM, F($\frac{2}{3}; 0)là trọng tâm tam giác AMN và điểm M có hoành độ âm. Tính tổng hoành độ các đỉnh B có thể xảy ra của hình vuông.

A. $\frac{2}{13}$
B. $\frac{8}{25}$
C. $\frac{7}{5}$
D. $\frac{11}{4}$

Câu 49: Tìm giá trị của a để hệ bất phương trình $\left\{\begin{matrix}|x+1| + |y+1| \leq a\\ |x-1| + |y-1| \leq a \end{matrix}\right.$

A. a = – 4
B. a = – 2
C. a = 1
D. Không tồn tại

Câu 50: Tìm tổng tất cả giá trị của m để hệ phương trình $\left\{\begin{matrix}m + x^{2} \leq 4x\\ m + 2x \geq x^{2}\end{matrix}\right.$

A. 4
B. B
C. C
D. 1

Xem đáp án

36 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Giải bài tập Đại số lớp 10 chi tiết, dễ hiểu