Dạng 3: Tìm điều kiện của tham số để hàm số đồng biến trên một khoảng

Dạng 3: Tìm điều kiện của tham số để hàm số đồng biến trên $(a;b)$.

Bài làm:

I. Phương pháp giải:

Hàm số đã cho đồng biến trên khi và chỉ khi $f^{\prime }(x)\ge 0$, $\mathrm{\forall }x\in (a;b)$.

Giả sử tương đương với $g(x)\ge m$ ( $m$ là tham số của bài toán).

Khi đó, yêu cầu của bài toán trở thành:

(1).

Ta có thể giải (1) bằng phương pháp hình học

• Đầu tiên ta vẽ đồ thị hoặc lập bảng biến thiên của hàm số , $x\in (a;b)$;
• Điều kiện (1) tương đương với: đồ thị (C) nằm từ đường thẳng trở lên.

II. Bài tập áp dụng

Bài tập 1: Tìm tất cả các giá thực của sao cho hàm số $y=2x^3-m{x}^2+2x$ đồng biến trên khoảng $(-2;0)$?

Bài giải: Ta có . Yêu cầu của bài toán tương đương với:

.

Xét hàm .

Ta có .

.

Ta có bảng biến thiên

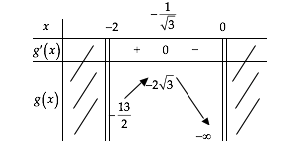
Suy ra .

Bài tập 2: Tìm tất cả các giá thực của sao cho hàm số $y=x^3+2x^2+mx+2$ nghịch biến trên khoảng $(-1;1)$?

Bài giải: Ta có . Yêu cầu của bài toán tương đương với:

.

Xét hàm .

Ta có bảng biến thiên:

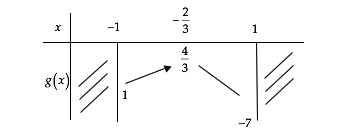
Vậy