Giải bài 1: Sự đồng biến, nghịch biến của hàm số

Bài đầu tiên chúng ta học về tính đơn điệu của hàm số, ứng dụng của đạo hàm để tìm tính chất đơn điệu của hàm số. Bài học này khá quan trọng vì nó móc xích trực tiếp đến các bài học sau của chương này và một số chương sau.

A. Lí thuyết

I. Tính đơn điệu của hàm số

Định nghĩa: Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.

Hình dáng đồ thị:

• Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.
• Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.

Ví dụ: Với hàm số có đồ thị như hình vẽ

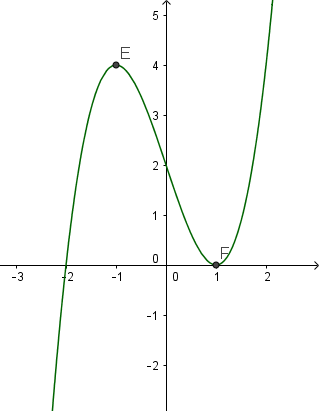
thì hàm số đồng biến trên khoảng , hàm số nghịch biến trên khoảng (-1,1).

II. Tính đơn điệu và dấu của đạo hàm

1. Định lí

Đinh lí: Cho hàm số có đạo hàm trên K.

a) Nếu với mọi x thuộc K thì hàm số f(x) đồng biến trên K.

b) Nếu với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

Chú ý: Mở rộng định lí: Giả sử hàm số có đạo hàm trên K. Nếu $f'(x) \geq 0$ ($f'(x) \leq 0$) với mọi x thuộc K và $f'(x)=0$ chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.

2. Quy tắc xét tính đơn điệu của hàm số

• Bước 1: Tìm tập xác định
• Bước 2: Tính đạo hàm f'(x). Tìm các điểm (i=1,2,...,n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
• Bước 3: Sắp xếp các điểm theo thứ tự tăng dần và lập bảng biến thiên.
• Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Ví dụ: Xét sự đồng biến nghịch biến của hàm số

Giải: Hàm số xác định với mọi . Ta có $$y'=x^{2}-x-2=0 \Leftrightarrow \left[ \matrix{x=-1\hfill \cr x=2 \hfill \cr} \right.$$

Bảng biến thiên

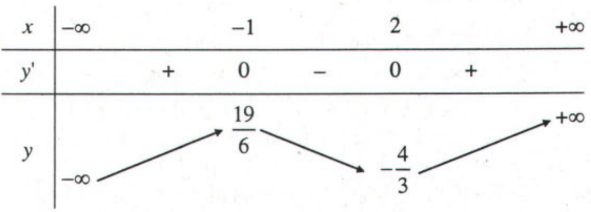
Vậy hàm số đồng biến trên khoảng và nghịch biến trên khoảng (-1,2).