Giải bài 1: Lũy thừa

Mở đầu chương 2 giải tích 12 với bài học Lũy thừa.Một kiến thức không quá khó song đòi hỏi các bạn học sinh cần nắm được lý thuyết. Dựa vào cấu trúc SGK toán lớp 12, KhoaHoc sẽ tóm tắt lại hệ thống lý thuyết và hướng dẫn giải các bài tập 1 cách chi tiết, dễ hiểu. Hi vọng rằng, đây sẽ là tài liệu hữu ích giúp các em học tập tốt hơn

A. Tổng hợp kiến thức

I. Khái niệm lũy thừa

1. Khái niệm

Cho n là một số nguyên dương.

Với a là số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a.

Chú ý: Trong biểu thức :

• a gọi là cơ số
• n gọi là số mũ
• Với a khác 0, ta có:
• 
• 
• Đặc biệt: ; $0^{-n}$ không có ý nghĩa.

2. Phương trình

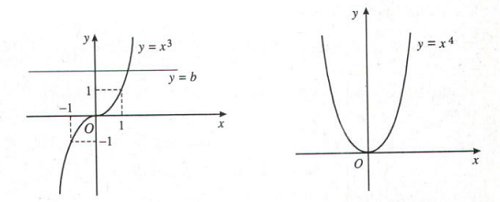
Biện luận số nghiệm của phương trình

TH n lẻ:

• Với mọi số thực b, phương trình có nghiệm duy nhất.

TH n chẵn:

• => phương trình vô nghiệm.
• => phương trình có một nghiệm $x=0$.
• => phương trình có hai nghiệm trái dấu.

3. Căn bậc n

Cho số thực b và số nguyên dương . Số a được gọi là căn bậc n của số b nếu $a^{n}=b$.

Ví dụ:

Khi đó:3 là căn bậc 2 của 9.

Biện luận số nghiệm của phương trình :

TH n lẻ và

• Phương trình có duy nhất một căn bậc n của b.
• Ký hiệu:

TH n chẵn

• => Không tồn tại căn bậc n của b.
• => Có một căn bậc n của b là số 0.
• => Có hai căn trái dấu, là $\pm\sqrt[n]{b}$.

Các tính chất của căn bậc n:

4. Lũy thừa với số mũ hữu tỉ

Cho số thực a dương và số hữu tỉ , trong đó $m \in Z$, $n \in N^{*}$. Lũy thừa của a với số mũ r là số $a^{r}$ xác định bởi:

5. Lũy thừa với số mũ vô tỉ

• Ta gọi giới hạn của dãy số là lũy thừa của a với số mũ $\alpha$.
• Ký hiệu:

với $\alpha =\lim_{n \to +\infty }r_{n}$

Chú ý:

II.Tính chất của lũy thừa với số mũ thực

Cho a, b là những số thực dương; , $\beta$ là những số thực tùy ý. Khi đó, ta có:

Nếu => $a^{\alpha }>a^{\beta }<=> \alpha >\beta $ Nếu => $a^{\alpha } \alpha >\beta $