Giải bài 4: Hàm số mũ. Hàm số Lôgarit
Bài học với nội dung kiến thức về Hàm số mũ, hàm số Lôgarit. Một kiến thức không quá khó song đòi hỏi các bạn học sinh cần nắm được lý thuyết. Dựa vào cấu trúc SGK toán lớp 12, KhoaHoc sẽ tóm tắt lại hệ thống lý thuyết và hướng dẫn giải các bài tập 1 cách chi tiết, dễ hiểu. Hi vọng rằng, đây sẽ là tài liệu hữu ích giúp các em học tập tốt hơn
A. Tổng hợp kiến thức
I. Hàm số mũ
1. Định nghĩa
- Cho a là số thực dương , khác 1.
- Hàm số
 được gọi là hàm số mũ cơ số a.
được gọi là hàm số mũ cơ số a.
2. Đạo hàm hàm mũ
Định lí 1
- Hàm số
 có đạo hàm tại mọi x .
có đạo hàm tại mọi x .
- Với hàm hợp, ta có công thức đạo hàm tương tự:
Định lí 2
- Hàm số
 , $a>0,a\neq 1$ có đạo hàm tại mọi x.
, $a>0,a\neq 1$ có đạo hàm tại mọi x.
- Với hàm hợp, ta có:
3. Khảo sát hàm số mũ ![]() ($a>0,a\neq 1$)
($a>0,a\neq 1$)
Tương tự bài toán khảo sát hàm số đã học:
- Tập xác định, sự biến thiên hàm số

- Lập bảng biến thiên
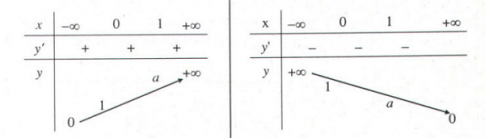
- Đồ thị hàm số
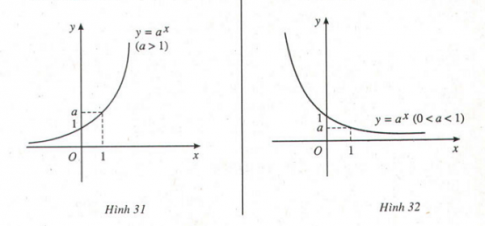
II. Hàm số Lôgarit
1. Định nghĩa
- Cho a là số thực dương , khác 1.
- Hàm số
 được gọi là hàm số Lôgarit cơ số a.
được gọi là hàm số Lôgarit cơ số a.
2. Đạo hàm hàm lôgarit
Định lí 3
- Hàm số
 ($a>0,a\neq 1$) có đạo hàm tại mọi $x>0$
($a>0,a\neq 1$) có đạo hàm tại mọi $x>0$
- Đặc biệt:

- Với hàm hợp, ta có công thức tương tự:
3. Khảo sát hàm số lôgarit
- Tập xác định, sự biến thiên hàm số

- Lập bảng biến thiên
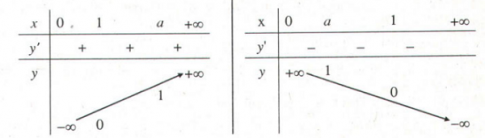
- Đồ thị hàm số lôgarit
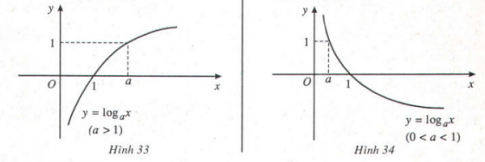
Một số công thức đạo hàm cần ghi nhớ

B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
Câu 1:Trang 77 - sgk giải tích 12
Vẽ đồ thị của các hàm số sau:
a) ![]()
b) ![]()
Câu 2: Trang 77 - sgk giải tích 12
Tính đạo hàm của các hàm số:
a) ![]()
b) ![]()
c) ![]()
Câu 3: Trang 77 - sgk giải tích 12
Tìm tập xác định của các hàm số:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Câu 4: Trang 78 - sgk giải tích 12
Vẽ đồ thị của các hàm số:
a) ![]()
b) ![]()
Câu 5: Trang 78 - sgk giải tích 12
Tính đạo hàm của các hàm số:
a) ![]()
b) ![]()
c) ![]()
Phần tham khảo mở rộng
Dạng 1: Tìm giới hạn của các hàm số mũ và lôgarit
Dạng 2: Dùng tính đơn điệu để chứng minh bất đẳng thức chứa mũ và lôgarit.
Chứng minh bất đẳng thức: ![]() tương tự cho $\leq ; \geq ;
tương tự cho $\leq ; \geq ;
=> Câu hỏi và bài tập trắc nghiệm toán 12 bài 4: Hàm số mũ và hàm số lôgarit











