Dạng 2: Dùng tính đơn điệu để chứng minh bất đẳng thức chứa mũ và lôgarit

Dạng 2: Dùng tính đơn điệu để chứng minh bất đẳng thức chứa mũ và lôgarit.

Chứng minh bất đẳng thức: tương tự cho $\leq ; \geq ;

Bài làm:

I. Phương pháp giải:

1. Chuyển bất đẳng thức đã cho về dạng: tương tự cho $\leq ; \geq ;
2. Tìm tập xác định của hàm số y=h(x).
3. Tính đạo hàm y'=h'(x), giải phương trình h'(x)=0.
4. Lập bảng biến thiên. Từ đó suy ra được bất đẳng thức cần chứng minh.

II. Bài tập áp dụng

Bài tập 1: Chứng minh bất đẳng thức:

Bài giải: Ta có .

Xét hàm số với $x\in [\frac{1}{2};1].$

Ta có

.

Ta có bảng biến thiên

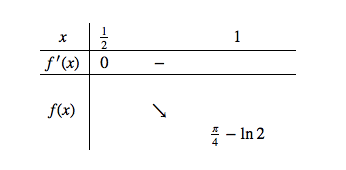
Từ bảng biến thiên ta được

Vậy

Bài tập 2: Chứng minh

Bài giải: Xét hàm số với $x\in [0; +\infty)$.

Ta có: với $x\in [0; +\infty)$.

đồng biến trên $[0; +\infty)$ $\Rightarrow f(x)>f(0) $ với $\forall x>0$.

Vậy hay $e^x >1+x$ (điều phải chứng minh).